Wir basteln uns ein Beugungsscheibchen

Nachdem die Diskussion über Beugungsbegrenzung und Beugungsscheibchen eine nie versiegende ist, wollen wir uns zur Abwechslung mal selber so ein Scheibchen basteln, und bei der Gelegenheit auch gleich die Wellenlänge des Lichts messen:

Alles, was wir dazu brauchen, ist:

• Ein Laserpointer
• Eine Nadel
• Ein Stückchen Alufolie
• Ein paar Meter Platz in einem (möglichst) dunklen Raum
• Eine weiße Wand oder ein Blatt weißes Papier an der Wand
• Ein Lineal

Zunächst wickeln wir die Alufolie über die Austrittsöffnung des Laserpointers und stechen dann mit der Nadel ein möglichst kleines Loch als Blende in die Folie (Abb. 1). Je kleiner das Loch, desto größer der Durchmesser der Beugungsringe. Allerdings: Je kleiner das Loch wird, umso weniger Licht kommt durch, was wiederum die Beobachtung erschweren kann.

Wir richten den Laserpointer jetzt auf eine weiße Wand in einem möglichst dunklem Raum und schalten den Laserpointer ein. Und – Tataaaa!!! – unser Beugungsscheibchen erscheint an der Wand.
 

Abbildung 1: Laserpointer mit Nadelloch als Blende in Alu-Folie

 
Bei einer Wellenlänge des Lasers von λ=635 nm und einem Durchmesser des Lochs in der Alufolie von D=0,5 mm und einem Abstand zur Wand von R=3 m würde der erste dunkle Ring einen Radius von
 

 
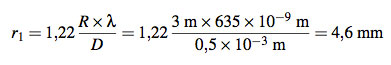
haben.

Und wenn Sie sich immer schon gefragt haben sollten, wie man die Wellenlänge des Lichts misst: Machen Sie es doch einfach selber, indem Sie diese Beziehung umdrehen: Zunächst benötigen wir dafür den Durchmesser D der Blende. Dazu fotografieren wir z.B. das Nadelloch zusammen mit einem Lineal mit einem (Makro-)Objektiv (Abb. 2). Mit dem Lineal oder – noch besser – dem Durchmesser des Laserpointers als Referenzgröße können wir dann den Durchmesser des Nadellochs am Monitor ausmessen (hier D=0,36 mm).
 

Abbildung 2: Vermessung des Durchmessers des Nadellochs (D=0,36 mm)

 
Wir richten nun den Laserpointer auf das Lineal, das wir an einer möglichst weit entfernten Wand (hier R=5132 mm) befestigt haben und messen im Beugungsbild (Abb. 3) mit dem Lineal den Durchmesser des ersten dunklen Rings (in Abb 3: 9,5+13 mm) bzw. dessen Radius r₁=(9,5+13)/2=11,25 mm
 

Abbildung 3: Beugungsbild des Nadellochs aus Abb. 2 in ca. 5 m Entfernung. Die sehr große Ausdehnung des Beugungsscheibchens und die nicht ganz runde Struktur des Nadellochs werden deutlich sichtbar.

 
Damit haben wir nun alles zusammen, was wir brauchen, um die Wellenlänge des Lasers zu messen als
 

 
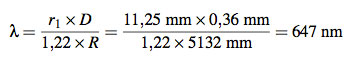
was trotz des primitiven (und ungenauen) Messaufbaus ziemlich gut dem Wert der Technischen Daten (635 nm) entspricht.

Für genauere Messungen der Wellenlänge von Licht wird man statt einer Blende ein Gitter verwenden, bei dem jeder Abstand der „Gitterstäbe“ als Blende fungiert. Das Wellenlängenspektrum wird auf diese Weise aufgefächert und statt auf einem Lineal auf einem Sensor abgebildet. (Dieser „Aufspaltungseffekt“ lässt sich an jeder CD beobachten, wo die Bits und Bytes optisch betrachtet ein Beugungsgitter bilden.)

Wenn wir nun die Wellenlänge des Lichts sowie den Abstand von der Blende zum Schirm kennen, können wir den Durchmesser des Blende zurückrechnen. Das ist in dem vorliegenden Fall natürlich nicht sonderlich originell, hat aber in der Wissenschaft eine sehr große Bedeutung: Wenn wir Licht hinreichend kurzer bekannter Wellenlänge, also Röntgenstrahlen, nehmen, lässt sich der Abstand von Atomen und somit die Struktur von Molekülen beobachten. Diese sogenannte Röntgendiffraktion ist eins der Arbeitspferde in Chemie, Pharmazie, Geologie, Mikrobiologie, Materialwissenschaft, Zementindustrie, etc.

Die vielleicht berühmteste Entdeckung, die – neben der Entdeckung der Atome an sich – auf diese Weise gemacht wurde, ist die Entschlüsselung der Struktur der DNS, dem Träger des Erbguts.

(Randolf Butzbach)
 
 
Anmerkung: Unsere kleine Bastelei ist nur das Vorgeplänkel zu einem umfangreichen Artikel zu den Grenzen der Auflösung, der heute um 16:15 Uhr online geht:

Von Megapixeln: Viel hilft viel