 Oder: Warum Thomas Maschke Unrecht hat und die weit verbreitete Sorge, der Sensor könnte eine höhere Auflösung haben als das Objektiv, selbst dann unbegründet ist, wenn sie zutreffend ist:
Oder: Warum Thomas Maschke Unrecht hat und die weit verbreitete Sorge, der Sensor könnte eine höhere Auflösung haben als das Objektiv, selbst dann unbegründet ist, wenn sie zutreffend ist:
Mit dem Erscheinen der Nikon D800/E mit ihren 36 Megapixeln auf Leica-Format (vulgo: Kleinbild, Vollformat, FX), der Sony Alpha 77 mit 24 Megapixeln auf APS-C, der Sony RX100 mit ihren 20 Megapixeln auf 1-Zoll-Sensor, oder dem Handy Nokia 808 mit fast 42 Megapixeln ist die Diskussion um die Grenzen der Auflösung voll entflammt: Für diese hohe Auflösung gäbe es doch gar keine Objektive mehr, sagen die einen. Die anderen argumentieren etwas hilflos, dass es vor vielen Jahren mal einen Film namens Agfa-Ortho 25 gab, mit einer extrem hohen Auflösung, und da hätte schließlich auch keiner nach der Qualität der Objektive gefragt. Dazwischen liegen diejenigen, die mit ihren MicroFourThirds- oder gar Kompakt-Kameras, die ein sehr feines Pixelraster haben (vgl. Tab. 1), überraschenderweise brauchbare Bilder erhalten – was gemäß der weit verbreiteten Meinung zum Thema Auflösung eigentlich undenkbar ist.
| µm | MP | mm2 | Format | Modelle, beispielhaft |
| 8,5 | 12 | 24×36 | KB | D700 |
| 8,0 | 6 | 15,8×23,6 | DX („APS-C“) | D70 |
| 6,0 | 24 | 24×36 | KB | a900, D3X |
| 5,2 | 80 | 40,4×53,7 | MF 645 | IQ180 |
| 4,9 | 36 | 24×36 | KB | D800/E |
| 4,0 | 24 | 15,8×23,6 | DX („APS-C“) | a77, NEX-7 |
| 3,7 | 16 | 13,0×17,3 | MFT | GH2, OM-D |
| 2,4 | 20 | 13,2×8,8 | CX | RX100 |
| 2,0 | 10 | 5,6×7,4 | 1/1,63“ | XZ-1, LX-5 |
| 1,4 | 42 | 7,5×10,8 | 1/1,2“ | Nokia 808 |
| 1,3 | 16 | 4,7×6,2 | 1/2,33“ | FS45, WB100 |
| 1,1 | Smartphone |
Tabelle 1: Die Pixelgröße verschiedener (mehr oder weniger) aktueller Kameras.
„Wieviele Megapixel verkraftet eine Kamera?“ fragte Thomas Maschke hier kürzlich und kam zu dem Schluss, „dass 16 Megapixel bei MicroFourthirds – ebenso wie 24 Megapixel im APS-C-Format – schon sehr sportlich sind“.
Die richtige Antwort hätte jedoch gelautet: „Je mehr (Megapixel und Dynamikumfang), desto besser!“
Verwirrend?
Dann der Reihe nach:
Die Auflösungsgrenze des perfekten Objektivs
In den folgenden Betrachtungen gehen wir davon aus, dass wir ein perfektes Objektiv haben, das keinerlei Abbildungsfehler aufweist. Auch gehen wir davon aus, dass unser Bildpunkt ein perfekter Punkt ist, also ohne Ausdehnung, mit 100 % Helligkeit im Punkt selber und direkt daneben 0 % Helligkeit. Um die Betrachtungen weiterhin zu vereinfachen, beschränken wir uns auf streng monochromatisches Licht, also Licht nur einer einzelnen Wellenlänge. Diese Situation werden wir in der Praxis so natürlich niemals vorfinden. Sie hilft uns aber beim Verständnis der Situation: Wenn wir alles weglassen, was die Auflösung offensichtlich begrenzt – gibt es dann eine Grenze der Auflösung und, wenn ja, wo liegt sie?
Diese gedachte letztgültige Grenze bezeichnen wir in der Physik als „theoretische Grenze“. Der Begriff unterscheidet sich entschieden von dem gleichen Begriff der Alltagssprache, wo der Ausdruck „theoretische Grenze“ gleichbedeutend ist mit angenommene, vermutete, vermeintliche, oder hypothetische Grenze. Hier geht es dagegen um eine letztgültige Grenze, die eigentlich nur in unserer perfekten, vereinfachenden Gedankenwelt erreichbar ist.
Auch die im Folgenden gezeigten perfekten Bilder existieren eigentlich nur in unserer Gedankenwelt. In der Realität werden viele andere Effekte, wie z.B. Linsenfehler, die Bilder überlagern. All das ist in den gerechneten Bildern nicht berücksichtigt worden. Die Bilder sind auf den jeweiligen zu zeigenden Einfluss des Bildes reduziert. Sie stellen somit die Situation in einer perfekten Welt dar.
Kann nun also ein perfektes Objektiv unendlich hoch auflösen, oder gibt es eine letzte Grenze, wo nichts mehr geht, selbst wenn alles perfekt sein sollte? – Ja, es gibt eine solche Grenze: Auch wenn die Linse selber perfekt sein sollte: Sie ist nicht unendlich groß. Irgendwo hat sie einen Rand und eine Fassung – selbst wenn die Linse einen Durchmesser von 39,3 m hat, wie z.B. das European Extremely Large Telescope (E-ELT) der Europäischen Südsternwarte. Irgendwo ist Schluss: Auch wenn alles andere perfekt sein sollte – um den Rand kommen wir nicht herum: Und diese Begrenzung des Linsendurchmessers ist es, die die Auflösung letztgültig begrenzt (und die der Hauptgrund für die derart großen Durchmesser von Teleskopen ist).
Wenn wir also einen perfekten Punkt durch unsere Optik abbilden wollen, werden wir es trotz perfekter Optik nicht schaffen, diesen perfekten Punkt als perfekten Punkt abzubilden: Der Punkt wird durch die begrenzte Größe des Strahlengangs verbreitert. Der Grund dafür ist, dass die Lichtwelle um Hindernisse herumlaufen, also in den Schattenraum eindringen kann. Diese Beobachtung wurde bereits 1665 (Datum der Veröffentlichung) von Francesco Maria Grimaldi (1618 – 1663) beschrieben und ist allgemein als Beugung bekannt.
Scheinbar unabhängig davon beschrieb Christiaan Huygens 1690 den der Beugung zugrundeliegenden Mechanismus, der als Huygenssches Prinzip bekannt ist: Man kann jeden Punkt einer Welle als Überlagerung von unendlich vielen dicht nebeneinander liegenden sogenannten „Elementarwellen“ ansehen, die sich derart gegenseitig überlagern, dass wir die bekannte Wellenfront sehen. Trifft nun eine Wellenfront auf ein Hindernis, ist dieser Überlagerungsmechanismus gestört, und die Elementarwelle kann sich ungehindert in den Schattenraum hinter dem Hindernis ausbreiten.
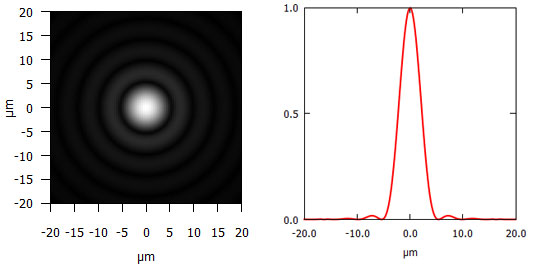
Abbildung 1: Beugungs- oder Airyscheibchen, bei 550 nm Wellenlänge des Lichtes (grün) und Blende 8.
Abb. 1 zeigt, wie das Bild des perfekten Punktes verbreitert wird, wenn die Auflösung durch die eben besprochene Beugung begrenzt ist. In der Mitte haben wir ein starkes Maximum, dann fällt die Intensität nach außen hin stark bis auf Null ab, steigt dann wieder an, aber bei weitem nicht so stark wie im Zentrum, fällt wieder auf Null ab und so weiter und so fort, bis ins Unendliche – oder bis der Bildausschnitt zu Ende ist.
Wie breit ist nun das Punktbild? Es gibt zwar keine natürliche Begrenzung des Punktbildes außer dem Bildausschnitt, allerdings wird die Intensität irgendwann so schwach, dass wir es nicht mehr wahrnehmen können, wo wir sagen: Hier ist kein Beugungsbild mehr zu sehen. In Abb. 1 ist der dritte Ring noch deutlich erkennbar, der vierte nur noch wahrnehmbar und beim fünften Ring (in den Ecken) fängt schon das „Kaffeesatzlesen“ an. Der Übergang zwischen Beugungsscheibchen und Nicht-Beugungsscheibchen ist also fließend. Wie sollen wir dann die Breite messen?
Nun, das hängt davon ab, was wir mit dem Zahlenwert machen wollen. Meistens misst man die volle Breite beim halben Maximalwert. Das geht normalerweise einfach und entspricht auch unserer intuitiven Vorstellung von Breite. Für manche Zwecke kann es dagegen günstiger sein, die halbe Breite bei 61 % zu messen, weil sie dann der Standardabweichung entspricht. Für andere Zwecke ist es sinnvoller, die Breite bei 10 % und/oder 90 % zu messen. Wir sehen schon: Die Definition der Breite ist vollkommen willkürlich und hat mehr mit äußeren Umständen als mit der Kurve selbst zu tun.
Das Beugungsbild des Punktes, auch Beugungs- oder (nach George Biddell Airy (1801-1892), der es erstmals berechnet hat) Airy-Scheibchen genannt, nimmt dagegen eine gewisse Sonderstellung ein: Die Berechnung dieses Beugungsbildes ist „per Hand“ extrem aufwendig und wurde erst durch den Einsatz von Computern und mathematischen Bibliotheken normal handhabbar.
Dagegen ist die Berechnung der Lage des ersten Beugungsminimums des Airy-Scheibchens ein Klacks: Der Ring des ersten Beugungsminimums hat einen Radius von
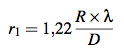
wobei R den Abstand der Blende zum Schirm/Film, λ die Wellenlänge des Lichts und D den Durchmesser der Blende bezeichnet.
Wenn wir nun als Abstand R die Brennweite f annehmen (was nicht vollkommen falsch ist bei symmetrischen Objektiven und Fokussierung auf Unendlich) und berücksichtigen, dass die sogenannte Numerische Apertur NA, also die Blendenzahl, sich als Verhältnis von Brennweite f zu Blendendurchmesser D ergibt, erhalten wir
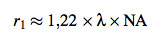
Und damit haben wir einen sehr einfachen Ausdruck für den Radius des ersten Beugungsminimums. Ein Ausdruck, der sehr viel einfacher zu messen ist, als die Breite des Beugungsbildes bei 50 % Maximalwert – zumal wir den Wert des Maximums hier gar nicht kennen müssen. Folglich bietet sich dieser Wert geradezu an, als Maß für die (halbe) Breite des Beugungsscheibchens. Wichtig ist aber, im Hinterkopf zu behalten, dass dieses Maß vollkommen willkürlich gewählt wurde, und dass das Beugungsscheibchen sich ausbreitet, bis es nicht mehr wahrnehmbar ist oder am Rand des Films bzw. Sensors abgeschnitten wird.
Zwei Beugungsscheibchen
Was passiert nun, wenn wir einen zweiten Punkt auf dem Film abbilden? Dumme Frage: Zwei Bilder natürlich, wie in Abb. 2a gezeigt.
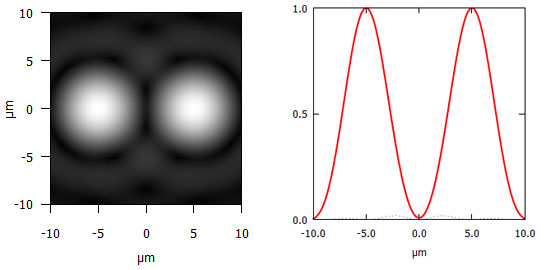
Abbildung 2a: Zwei Beugungsscheibchen im Abstand von 10 µm bei 550 nm (grün) und Blende 8.
Und wenn wir sie weiter zusammenrücken, wie z.B. in Abb. 2b gezeigt? Na, dann haben wir immer noch zwei Bilder. Aber Vorsicht! Die Ausläufer der beiden Beugungsbilder überlappen sich irgendwann nicht unwesentlich. In den Bereichen, wo die Intensitäten der einzelnen Beugungsbilder bereits auf 37 % abgefallen ist, summieren sich die beide Intensitäten zu stattlichen 73 % der Intensität im Zentrum: Der Dunkelraum zwischen den beiden Bildern hat sich mit Licht angefüllt und ist nur noch 27 % dunkler als die Maximalhelligkeiten und damit nur noch mehr oder weniger gut erkennbar.
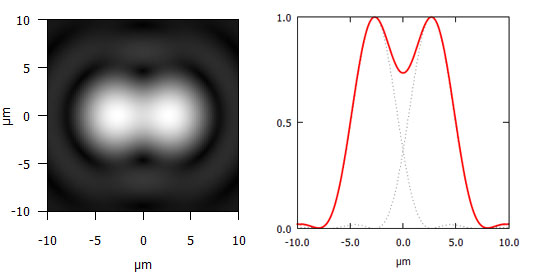
Abbildung 2b : Zwei Beugungsscheibchen im Abstand von 5,4 µm bei 550 nm (grün) und Blende 8. Das Rayleigh-Kriterium ist für diese Wellenlänge und Blende erfüllt. Die Intensität fällt zwischen den Maxima auf 73 % des Maximalwerts ab.
Wenn wir nun die beiden Beugungsbilder noch weiter zusammenschieben wie in Abb. 2c, läuft der Dunkelraum zwischen den beiden Beugungsbildern komplett zu und wir können die beiden Bilder nicht mehr auseinander halten. Es ist nur noch ein verbreitertes Beugungsbild erkennbar.
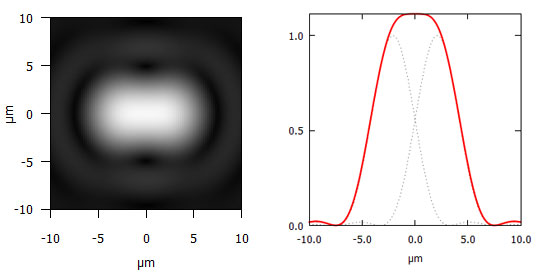
Abbildung 2c: Zwei Beugungsscheibchen im Abstand von 4,2 µm bei 550 nm (grün) und Blende 8: Es gibt kein Minimum zwischen den beiden Maxima mehr, mit denen die beiden Beugungsbilder unterscheidbar wären. Die absolute Auflösungsgrenze ist erreicht (Sparrow-Grenze).
Und wenn wir die Beugungsbilder nun noch weiter zusammenschieben, verschmelzen sie komplett und erscheinen als einzelner Punkt, wie in Abb. 2d gezeigt.
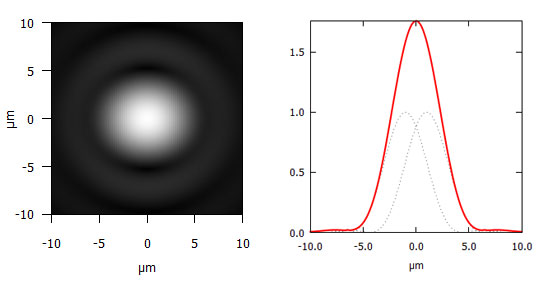
Abbildung 2d: Zwei Beugungsscheibchen im Abstand von 2 µm bei 550 nm (grün) und Blende 8: Die beiden Beugungsbilder können nicht mehr unterschieden werden und erscheinen als ein Punkt.
Der Übergang zwischen „klar voneinander unterscheidbar“ und „nicht mehr unterscheidbar“ ist also ebenfalls fließend. Zur Illustration ist in Abb. 3 der Kontrast zwischen Minimum und Maximum gegen den Abstand der Beugungsbilder aufgetragen:
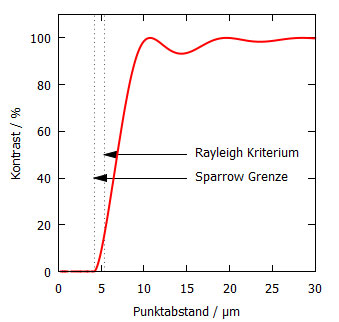
Abbildung 3: Der Kontrast zwischen den zwei Beugungsscheibchens aus Abb. 2, aufgetragen als Funktion des Punktabstands. Je enger die Punkte zusammenrücken, desto geringer wird der Kontrast zwischen den einzelnen Punkten, bis er irgendwann ganz verschwindet (Sparrow-Grenze). Das Rayleigh-Kriterium ist dagegen ein willkürlicher Punkt auf der Kurve.
Dabei ist der Kontrast definiert als
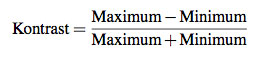
Wie viele Details wir schließlich erkennen, d.h. auflösen können, hängt dann davon ab, wie viel Kontrast wir (für das fertige, ausgedruckte und an der Wand hängende Bild) benötigen, um mit unserem Auge z.B. zwei Grashalme voneinander unterscheiden zu können.
Weil es grade so schön passt, kommt hier ein etwas abstrakterer Einschub: Für die Beschreibung der Auflösung werden in der Praxis statt der beschriebenen Punkte z.B. Linienmuster unterschiedlicher Periodenlängen verwendet, deren Helligkeit sich sinusförmig ändert, wie in Abb. 4 für verschiedene Periodenlängen skizziert: Die Helligkeitsänderung erfolgt also nicht sprunghaft von 0 % auf 100 %, sondern ändert sich sinusartig zwischen 0 % und 100 % wie in Abb. 4 a) gezeigt. Aber egal, ob wir nun Punkte oder sinusförmiges Streifenmuster abbilden: Die optischen Elemente „verschmieren“ den Kontrast: Die Unterschiede zwischen maximaler und minimaler Helligkeit sinken, je dichter die Linien zusammengepackt sind, also je kürzer die Periodenlänge bzw. je höher die Frequenz des Linienmusters ist. D.h. je mehr Linienpaare pro Millimeter abgebildet werden, desto „flauer“ ist der Kontrast, wie in Abb. 4 b) skizziert.
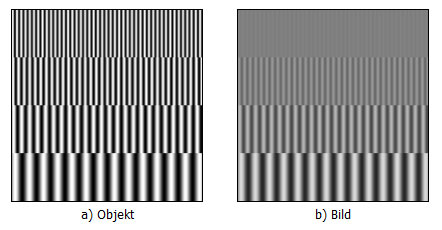
Abbildung 4: Streifenmuster mit sinusförmigem Helligkeitsverlauf unterschiedlicher Periode (a) werden durch ein optisches System mit verringertem Kontrast abgebildet (b). Dabei wird der Kontrast umso geringer je dichter die Linienpaare zusammenrücken bis sie nicht mehr unterscheidbar sind (Skizze).
Wir können jetzt die Maxima und Minima für jede Linienfrequenz ausmessen und in einem Diagramm den so ermittelten Kontrast (ähnlich Abb. 3) gegen die Anzahl der Linienpaare pro Millimeter auftragen, wie in Abb. 5 gezeigt.
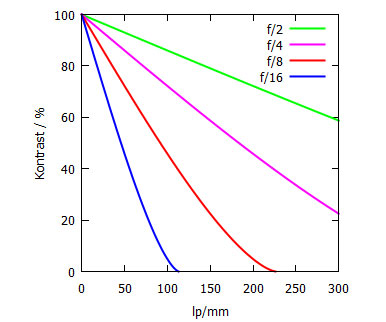
Abbildung 5: Die Modulationsübertragungsfunktion (MTF) einer einzelnen runden Blende bei 550 nm Wellenlänge des Lichtes und Blende 2, 4, 8 und 16. Man sieht, dass bei Blende 16 der Kontrast bei 50 lp/mm bereits auf ca. 50% abgefallen ist und er bei ca. 110 lp/mm dann komplett verschwindet, während man bei Blende 2 bei 300 lp/mm noch knapp 60 % Kontrast hat.
Die Kurve beschreibt also, was von einst 100 % Kontrast im Objekt (Abb. 4 a) nach der Abbildung der sinusförmigen Linien im Bild (Abb. 4 b) noch übrig bleibt. Diese Kurve heißt Kontrast- oder Modulationsübertragungsfunktion (MÜF) bzw. Englisch Modulation Transfer Function (MTF)Der Charme der MTF ist, dass man für jedes Element der Wiedergabekette eine solche MTF angeben kann, die man dann alle miteinander multiplizieren kann und so die gesamte Kontrastübertragung der Wiedergabekette erhalten kann. Das funktioniert allerdings nur für Sinusfunktionen – was uns also nichts nützt, weil so was im täglichen Leben ja wohl nur sehr selten vorkommt.
Wirklich?
Achtung, jetzt kommt’s ganz dicke: Joseph Fourier (1768 – 1830), dem man dafür gar nicht genug danken kann, hat herausgefunden, dass man jede Struktur – also auch unser Motiv bzw. Bild – als Überlagerung von Sinus-Funktionen, also Frequenzen, ansehen und beschreiben kann. Das Ergebnis dieser Umrechnung nennt sich dann vornehm (je nach Verfahren) Fourierreihe oder Fouriertransformation. Wir können folglich jedes Bild als Überlagerung von Sinusfunktionen betrachten, auf dessen Beschreibung im sogenannten Frequenzraum wir die MTF anwenden dürfen: Das ist der Grund, warum wir z.B. für die Messung der MTF Sinusfunktionen brauchen.
Aber zurück zu unseren anschaulicheren Beugungsscheibchen …
Nun habe ich die vier Versionen von Abb. 2 nicht ausschließlich zufällig ausgewählt. Insbesondere Abb. 2b beschreibt die Situation, wie sie allgemein diskutiert wird, wenn das Gespräch auf das Thema Auflösung kommt: Das Maximum des ersten Beugungsscheibchens fällt mit dem ersten Minimum des zweiten Beugungsscheibchens zusammen, was allgemein als Rayleigh-Kriterium bezeichnet wird. Nach allem, was wir bisher bereits wissen, ist mit dem Rayleigh-Kriterium nicht das Ende der möglichen Auflösung des Objektivs erreicht. Diesen Punkt sehen wir erst bei Bild 2c erreicht, wenn es kein Minimum zwischen den beiden Maxima mehr gibt: die sogenannte Sparrow-Grenze.
Warum redet dann alle Welt vom Rayleigh-Kriterium?
Ganz einfach: Erstens sind die Beugungsringe sehr leicht zu beobachten, und damit auszumessen: Ein Lineal reicht. Zweitens liegt im praktischen Leben zwischen Rayleigh-Kriterium und absoluter Auflösungsgrenze (Sparrow-Grenze) kein sehr großer Unterschied mehr. Als Auflösungsgrenze ist das Rayleigh-Kriterium vollkommen willkürlich gewählt, nur der Einfachheit der Berechnung geschuldet und als Abschätzung der Auflösungsgrenze nicht vollkommen falsch – besonders, wenn man, drittens, berücksichtigt, dass u.a. die Linsenfehler ja auch die Auflösung begrenzen (können). Oder, um es mit Lord Rayleighs eigenen Worten zu sagen:
(Diese Faustformel ist dank ihrer Einfachheit bequem, und sie ist hinreichend genau, angesichts der zwangsläufigen Unsicherheit, was mit Auflösung tatsächlich gemeint ist.)
Die Auflösungsgrenze hat also nur indirekt mit dem Beugungsscheibchen zu tun. Richtig gelesen: nur indirekt. Die Beugung sorgt zwar für eine Verbreiterung des Punktes – die Auflösung ist aber letztendlich dadurch begrenzt, wie gut wir das Minimum (sofern es noch vorhanden ist) noch auflösen können, also es von den Maxima unterscheiden können. Also, wie gut wir die „Delle“ zwischen den Punktbildern erkennen können: Wir können die Auflösung des Objektivs also nicht losgelöst von unseren Beobachtungsmöglichkeiten sehen.
Das ist nun der Punkt, wo unser Film oder Sensor ins Spiel kommt. Denn der hat einen entscheidenden Einfluss darauf, ob, und wenn ja, wie gut wir die „Delle“ zwischen den beiden Punktbildern aufzeichnen können. Wir können die Auflösungsgrenze des Objektivs also nicht losgelöst von der Auflösungsgrenze unserer Bildaufzeichnung betrachten.
Daher ist die Frage „Wie viele Megapixel verkraftet eine Kamera?“ ungefähr so sinnvoll wie die Frage „Wie viele Liter Benzin verkraftet ein Auto?“ Was dem Objektiv sein Sensor ist, ist dem Auto sein Benzin. Das eine ist nötig, um mit dem anderen etwas anfangen zu können. Ohne Benzin fährt kein Auto und ohne (wie auch immer gearteten) Sensor gibt es kein verteilbares und diskutierbares vom Objektiv erzeugtes Bild.
Schauen wir uns also nun den Einfluss des Sensors auf die Auflösung des Gesamtsystems Objektiv-Sensor an:
Der Einfluss des Sensors auf die Gesamtauflösung
Die Kontrastauflösung
Der erste Einfluss des Sensors ist die Intensitäts- oder Kontrastauflösung: Die Detektierung von Licht basiert auf dem Photoeffekt, für dessen Erklärung übrigens Albert Einstein 1921 seinen Nobelpreis bekommen hat: Wenn ein Lichtteilchen („Photon“) auf ein Elektron trifft kann es – genügend hohe Energie, d.h. Frequenz oder kurze Wellenlänge, vorausgesetzt – das Elektron aus seiner Bindung an den Atomkern herausschlagen.
Film
Beim Film geht dabei die lichtempfindliche chemische Verbindung im Wortsinn in die Brüche. Stark vereinfacht ausgedrückt, werden die so entstandenen Bruchstücke im Entwicklungsprozess eingefärbt und die verbliebenen ganzen Verbindungen vom Fixierer herausgewaschen.
Je größer nun diese Verbindungen sind, desto wahrscheinlicher ist es, dass ein Photon eine Verbindung trifft und zerstört. Es reichen also bereits wenige Photonen aus, „um Schaden anzurichten“, sprich, der Film wird umso grobkörniger, je empfindlicher er ist. (Was allerdings nicht heißt, dass jeder grobkörnige Film auch hochempfindlich ist…) Dagegen sind hochauflösende Filme, also solche mit sehr kleinem Korn, gleichzeitig auch unempfindlich.
Weiterhin ist es beim Film so, dass mit jeder zerstörten Verbindung eine Verbindung weniger bleibt, die lichtempfindlich ist. Das heißt, je stärker der Film bereits lokal belichtet ist, desto unempfindlicher wird er an dieser Stelle und die Schwärzung geht in Sättigung. Überbelichtete Spitzlichter werden also nicht radikal abgeschnitten, sondern laufen sanft aus.
Für die Auflösungsgrenze bedeutet das, dass die Kontrastkurve zwischen den Punktbildern flach wird, also dem Erkennen der „Delle“ zwischen den Punktbildern entgegen wirkt. D.h. wie gut der Film die beiden Punktbilder auseinanderhalten kann, hängt also auch davon ab, wie der Film belichtet wird: Wird der Film unter- oder überbelichtet, mag der Unterschied in der Anzahl der belichteten Verbindungen nicht groß genug sein, um die „Delle“ noch erkennen zu können.
Sensor
Anders stellt sich die Situation beim Sensor dar: Hier geht keine Verbindung kaputt. D.h. das einzelne Bildelement (Pixel) bleibt während der ganzen Zeit der Belichtung gleichmäßig empfindlich. Die Elektronen werden von ihrer Bindung an den Atomkern gelöst („Äußerer Photoeffekt“) und in einem Kondensator gespeichert. Das so dem Atom fehlende Elektron wird sofort über den Schaltkreis nachgeliefert. Eine andere Möglichkeit besteht z.B. darin, eine Photodiode unter dem Einfluss des Lichtes leitfähig zu machen („Innerer Photoeffekt“) und so einen Kondensator zu (ent)laden.
In beiden Fällen ist dann aber irgendwann plötzlich Schluss: Der Kondensator ist vollständig ge- bzw. entladen, was dazu führt, dass (überbelichtete) Spitzlichter schlicht abgeschnitten werden. Da Elektronen unteilbar sind, also eine diskrete Anzahl Elektronen gespeichert ist, werden beim Auslesen des Sensors die gespeicherten Elektronen ausgezählt. D.h. das im Sensor gespeicherte Signal ist bereits von Natur aus digital. Folglich ist es (abgesehen von Marketinggründen) sinnlos, die Bittiefe des sogenannten Analog-Digital-Wandlers (ADC) zu vergrößern, wie immer wieder in den Foren gefordert wird. Der ADC kann keine größere Anzahl verschiedener Werte abliefern, als im Sensor Elektronen „produziert“ und gespeichert werden können.
Wie man leicht sieht, zählt dabei das Verhältnis vom gewollten Signal zum sogenannte Helligkeitsrauschen, also der Belichtung des Pixels unter anderem durch Wärme (der Sensor ist nicht nur für sichtbares Licht empfindlich!), der statistischen Streuung der einfallenden Photonen und damit der erzeugten Elektronen (bei identischer Belichtung!), sowie von der Belichtungszeit unabhängige Störungen, die durch das Auslesen entstehen.
Um mal Butter bei die Fische zu geben, ein konkretes Beispiel: Der Kodak KAF-40000 Fullframe-CCD-Sensor, dessen Spezifikationen sich sehr gut mit denen der Pentax 645D decken, hat laut Datenblatt (PDF-Datei) eine Kapazität von 42.000 Elektronen pro Pixel. Der Rauschuntergrund besteht dagegen aus 13 Elektronen Ausleserauschen, was ein Signal-Rausch-Verhältnis von 42.000:13 oder 3231:1 ergibt. Hinzu kommt (bei 60° C Sensortemperatur) die wärmebedingte „Belichtung“ von 42 pA/cm2, d.h. 262 Millionen Elektronen pro Sekunde und Quadratzentimeter bzw., bei einer Pixelgröße von 6×6 µm2, 94 Elektronen pro Sekunde und Pixel. Dieser Wert verdoppelt sich alle 5,5° C: Bei 65,5° C sind es also schon 188 Elektronen/Sekunde, bei 71°C 376 Elektronen, usw. Bei einer angenommenen „Belichtungszeit“ von einer 1/50 Sekunde (also der Zeit zwischen letzten Löschen und Auslesen) ergäbe sich so bei 60°C Betriebstemperatur ein Wärmeanteil von ungefähr 2 Elektronen/Pixel. Zusammengenommen bedeutet das ein Signal-Rausch-Verhältnis von 42.000:(13+2) oder 2800:1. Damit hätten wir einen Dynamikumfang von 2800:1 oder 11,5 Blendenstufen, wie Kodak und Pentax ihn in den Technischen Daten kommunizieren.
Bei längeren Belichtungszeiten steigt der Wärmeanteil entsprechend. Hierbei hilft man sich damit, dass man den Wärmeanteil mit schwarz maskierten Pixeln an Bildrand misst und ihn dann nach der Belichtung vom eigentlichen Bild abzieht. Bei längeren Belichtungszeiten wird man nach der Aufnahme noch ein Bild mit der selben Belichtungszeit bei geschlossenem Verschluss aufnehmen und dieses Dunkelbild vom eigentlichen Bild abziehen. Besser ist natürlich, durch Kühlung dafür zu sorgen, dass der Wärmebeitrag möglichst klein bleibt, was aber bei Fotoapparaten weder praktikabel noch finanziell darstellbar ist.
Wenn wir die generierten Photoelektronen jetzt „digitalisieren“, dann brauchen wir zunächst z.B. einen 16-Bit-ADC, um die maximal 42.000 Elektronen aus dem Pixel voll darstellen zu können. Von den 16 Bit brauchen wir aber genau genommen nur 15,4 Bit. Davon sind die unteren 3,9 Bit mit den 15 Elektronen Auslese- und Wärmerauschen gefüllt, die wir sofort wegwerfen können, da sie keinerlei Information enthalten und uns somit auch nichts nützen. Übrig bleiben also wiederum nur – Überraschung!!! – 15,4-3,9=11,5 Bit echtes Signal, die wir platzsparend und verlustfrei in 12 Bit Datenbreite speichern können. Eine höhere Bittiefe bzw. Datenbreite wäre damit nur Verschwendung von Speicherplatz und erhöht die Speicher und Transferzeiten (Serienbilder!)) – – wobei es natürlich andererseits nichts schaden kann, die Datenbreite etwas größer auszulegen, um den statistischen Schwankungen im Rauschen Rechnung zu tragen: Die 13 Elektronen Ausleserauschen sind schließlich nur der Mittelwert.
Bleiben wir also für die folgende Betrachtung bei den 11,5 Blendenstufen bzw. Bit:
Für unsere Auflösungsgrenze bedeutet dies, dass bei perfekter Belichtung im Fall des Rayleigh-Kriteriums, dass wir in den Maxima einen digitalisierten Wert von 2800 haben und in der „Delle“ zwischen den beiden Punktbildern einen Wert von ca. 2050. D.h. es liegen ca. 750 Zählerwerte zwischen den Maxima und dem Minimum. Wir können die beiden Punktbilder also sehr gut voneinander unterscheiden.
Und auch wenn das Bild unterbelichtet sein sollte, bzw. wenn wir in die Schattenpartien des Bildes gucken, wo z.B. nur ein Zehntel des Maximums belichtet sein könnte, haben wir immer noch einen Zählerstand von 280 in den Maxima und von 205 im Minimum. Zwischen Maximum und Minimum liegen also immer noch ca. 75 Zählerwerte Abstand, die in der Weiterverarbeitung gestreckt werden können.
Ganz anders sieht die Welt aus, wenn wir das Bild z.B. in einer 8-Bit-JPEG-Datei speichern, die aufgrund der 8 Bit nur 256 verschiedene Werte pro Farbkanal annehmen kann: Hier würden in den Schattenpartien die Maxima einen Zählerstand von 25 erreichen und das Minimum würde bei 18 liegen., also grade mal 7 Zähler Unterschied. Der Wert läge also knapp über dem Rauschen, würde wohl weiterhin von JPEG-Artefakten überlagert, und sich vermutlich auch bei einer Kontrasterhöhung in der Bildbearbeitung nicht mehr sauber herausarbeiten lassen. Hinzu kommt, dass z.B. im sRGB-Farbraum die Schatten mit einem sogenannten gamma-Wert von 2,2 aufgehellt werden, damit sie dem natürlichen Seheindruck näher kommen. Diese Aufhellung erfolgte auch bei den hier gezeigten Beugungsbildern, um die Ringe um das Maximum im Zentrum erkennbar zu machen (vgl. Abb. 1). Abbildung 6 zeigt den Vergleich zwischen der linearen Helligkeitswiedergabe (gamma=1,0) und dem mit gamma=2,2 aufgehellten Bild.
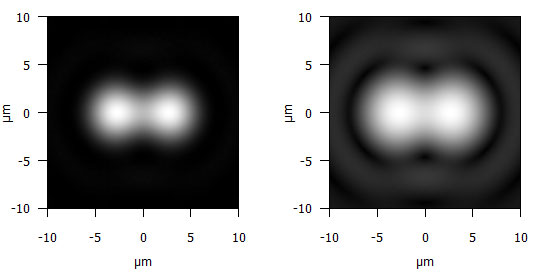
Abbildung 6: Der Einfluss der Gammafunktion auf die Unterscheidbarkeit von zwei Punkten: Links mit gamma=1,0, rechts mit gamma=2,2 wie im sRGB-Farbraum üblich.
Von Megapixeln: Viel hilft viel
Kommen wir nun zu dem meistdiskutierten Aspekt der Auflösung: Der Ortsauflösung des Sensors, oder, salopp gesagt, den Megapixeln.
Schauen wir uns zunächst den klassischen Fall an, in dem der Abstand der Bildpunkte größer ist als die Größe der Pixel und der Beugungsscheibchen. Im Beispiel in Abb. 7 befinden sich die Punkte wie in Abb. 2a in einem Abstand von 10 µm. Bei Verwendung eines 50-mm-Objektivs und bei einem Aufnahmeabstand von drei Metern entspricht dies einem Objektabstand von 0,6 mm, den wir hier abgebildet sehen. Das Bild ist mit einer Pixelgröße von 4 µm gerastert, was zum Beispiel 24 Megapixel auf APS-C entspricht. Wir können die beiden Punkte hier noch sauber unterscheiden.
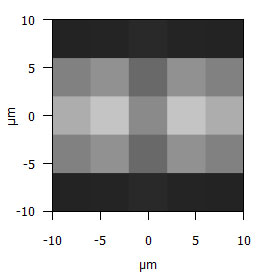
Abbildung 7: Die Beugungsbilder (550 nm, Blende 8) von zwei Punkten im Abstand von 10 µm bei einem Pixelraster von 4 µm: Die beiden Punkte können noch als zwei verschiedene Punkte erkannt werden.
Was passiert nun, wenn wir die Punkte auf das Rayleigh-Limit, also hier 5,4 µm bei Blende 8 und 550 nm Wellenlänge, zusammenschieben wie in Abb. 2b gezeigt? Abbildung 8 zeigt also dasselbe Bild wie Abb. 2b, jedoch mit 4 µm Sensorauflösung gerastert. Wie wir sehen, können wir jetzt die beiden Punkte nicht mehr unterscheiden. Sie verschmelzen zu einem einzelnen Punkt. Das ist der Fall, der in den Foren diskutiert wird: Er zeigt aber auch, dass uns das Rayleigh-Kriterium hier nicht weiterhilft als alleinige Definition der Auflösungsgrenze.
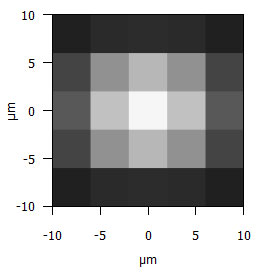
Abbildung 8: Die Beugungsbilder (550 nm, Blende 8) von zwei Punkten im Abstand von 5,4 µm (Rayleigh-Kriterium) bei einem Pixelraster von 4 µm: Die beiden Punkte verschmelzen zu einem Punkt und können nicht mehr als zwei verschiedene Punkte erkannt werden.
Was passiert aber nun, wenn wir uns nicht an das Rayleigh-Kriterium halten, und die Auflösung des Pixelrasters einfach weiter erhöhen, auf, sagen wir 1 µm, was laut gängiger Forenweisheit vollkommen sinnlos sein soll? Das Ergebnis sehen wir in Abb. 9:
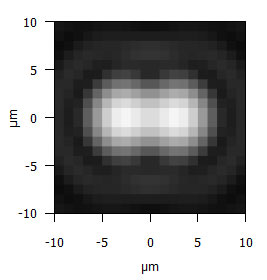
Abbildung 9: Dieselbe Situation (erfülltes Rayleigh-Kriterium) wie in Abb. 8, jedoch bei einem Pixelraster von 1 µm. Dank der hohen Auflösung können die beiden Punkte wieder als zwei verschiedene Punkte erkannt werden.
Wir können jetzt die „Delle“ zwischen den beiden Beugungsscheibchen wieder auflösen, und erkennen, dass es sich um zwei Punkte handelt statt einen, wie im Fall von Abb. 8 gezeigt.
Wenn wir das Raster nun noch weiter erhöhen (würden), auf sagen wir 0,1 µm, so erhalten wir Bild 2b: Denn nichts anderes stellt Bild 2b dar. Die für die Illustration dieses Artikels mit 0,1 µm gerasterte Summe der „analogen“ Airy-Funktionen.
Je höher die Pixelauflösung des Sensors ist, desto genauer kann also das Bild aufgezeichnet werden und desto feinere Informationen können herausgearbeitet werden.
Die Beschränkung der Diskussion auf Rayleigh-Kriterium und Pixelgröße, die angeblich größer sein muss als jenes, ist somit nur sehr grob, ähnlich wie ein Schnitzwerk mit der Axt.
Schlussfolgerung für den Sensor
Gilt also das Fazit: „Je mehr Megapixel pro Fläche, desto besser“?
Ja und nein. Ja, weil dann die Ortsauflösung des Sensors steigt. Nein, weil je mehr Pixel pro Quadratmillimeter untergebracht sind, desto kleiner wird die Pixeloberfläche und desto unwahrscheinlicher wird es, dass (wie beim Filmkorn) ein Photon in ein Pixel trifft – bei teilweise gleichbleibenden Störeinflüssen, also Beiträgen zum Rauschen. Das Pixel wird also unempfindlicher, während manche Störeinflüsse gleich bleiben und somit das Signal-Rauschverhältnis sinkt, was unserer Intensitäts-Auflösung entgegenwirkt.
Gilt also doch: Je größer die Pixel desto größer das Signal-Rauschverhältnis?
Auch hier haben wir wieder ein Ja-Aber: Denn je größer die Pixel werden, desto empfindlicher wird zwar das einzelne Pixel für das Licht (wie gewollt), aber gleichzeitig wird es auch (ungewollt) empfindlicher für Störeinflüsse wie z.B. Wärme. Das Signal-Rauschverhältnis verbessert sich also irgendwann nicht mehr. Das Einzige, was hilft, ist durch ein intelligentes Schaltungsdesign das Ausleserauschen möglichst gering zu halten und den Wärmeanteil aufwendig durch Kühlung zu reduzieren – wobei letzteres in einer Kamera selten praktikabel ist.
Die Hohe Kunst des Sensorbaus besteht also jetzt darin, die sich widerstrebenden Eigenschaften Ortsauflösung (Megapixel) einerseits und Intensitätsauflösung (Dynamikumfang) andererseits durch konstruktive Tricks zu „versöhnen“ und für die jeweilige Anwendung den besten Kompromiss aus beiden zu finden.
Jenseits des monochromatischen Beugungsscheibchens
Bisher haben wir andere wesentliche Einflüsse ausgeblendet. Allen voran sei hier erwähnt, dass unsere bisherigen Betrachtungen sich auf monochromatisches Licht einer mittleren Wellenlänge bezogen. In der Praxis hat man normalerweise statt einer einzelnen scharf definierten Wellenlänge weißes Licht bzw. ein größeres Wellenlängenintervall wie in Abb. 10 skizziert:
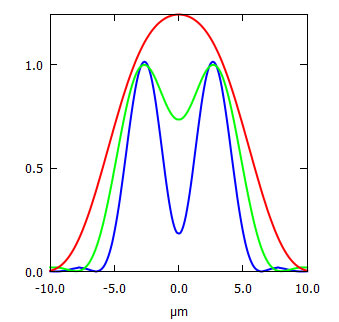
Abbildung 10: Überlagerung der Beugungsscheibchen von verschiedenen Wellenlängen bei Blende 8. Bei dem Punktabstand ist das Rayleigh-Kriterium für grünes Licht (grüne Linie) erfüllt, während rotes Licht (rote Linie) nicht mehr aufgelöst werden kann und die blauen Beugungsscheibchen (blaue Linie) noch sehr klar von einander unterscheidbar sind. Die praktisch beobachtbare Auflösung für weißes Licht ist also ein Mischung aus allen Wellenlängen. Aus Gründen der Klarheit wurden die einzelnen Beugungsbilder weggelassen und nur die Summe gezeigt.
In Abb. 10 ist – wie bisher diskutiert – das Rayleigh-Kriterium für grünes Licht erfüllt. Für blaues Licht dagegen ist bei gleichem Punktabstand das Rayleigh-Kriterium in weiter Ferne, während die beiden Punkte bei rotem Licht nicht mehr unterschieden werden können und zu einem Punkt verschmelzen.
Dabei bezieht sich Abb. 10 ausschließlich auf das Beugungsscheibchen. Im Fall von Glasoptiken (Objektiven) muss man in der Praxis weiterhin z.B. die Dispersionseigenschaften des Glases berücksichtigen, also wie stark sich der Brechnungsindex des Glases in Abhängigkeit von der Wellenlänge ändert – und damit wie unterschiedlich stark die einzelnen Farben des Lichtstrahls abgelenkt werden. Dabei kann es z.B. passieren, dass der Auflösungsvorteil des Beugungsscheibchens am blauen Ende durch die Dispersionseigenschaften des Glases wieder zunichte gemacht wird.
Auch hier ist also der Übergang von klar aufgelöst zu nicht aufgelöst fließend. Man wird aber immer alle Beugungsbilder der einzelnen Wellenlängen / Farben gleichzeitig sehen, bzw. auf dem Sensor aufzeichnen.
Und das bringt uns nun zu der Farbempfindlichkeit des Sensors. Der Bayer-Sensor „sieht“ bekanntlich nur jedes zweite Pixel in der selben Farbe, wobei der einzelne Farbkanal sauber definiert ist. Beim Foveon-Sensor wird dagegen jeder Farbkanal mit jeder Farbe belichtet – nur unterschiedlich stark gewichtet und die nachfolgende Mathematik muss daraus die Farbinformationen extrahieren. Die Beurteilung, welches Verfahren die besseren Ergebnisse liefert, liegt weit jenseits dieses Beitrags.
Auch haben wir andere reale Einflüsse wie z.B. Abbildungsfehler oder den Antialias-Filter (sofern vorhanden) ausgeblendet. Als weitere Schritte müssten wir beim Sensor die Gradationskurve bzw. die Stellung der Kontrastregler im Bildbearbeitungsprogramm sowie die Wiedergabefunktion des Druckers und Papiers berücksichtigen. Im Fall des Films beeinflussen das Vergrößerungs- bzw. Projektionsobjektiv sowie die Gradationskurve des Fotopapiers die Auflösungsgrenze. Und schließlich und endlich hat auch unser Auge eine Wiedergabefunktion mit nachgeschalteter extrem leistungsfähiger „Bildverarbeitung“.
Es gibt aber keine Rayleigh-Grenze (wie hier unterstellt), ab der von jetzt auf sofort nichts mehr aufgelöst wird. Stattdessen nimmt der Kontrast der (immer gröberen) Details immer mehr ab, bis bei der Sparrow-Grenze der Kontrast bei 0 % angelangt ist und somit keine Details mehr unterscheidbar sind. Es gibt also keinen scharfen Übergang zwischen „aufgelöst“ und „nicht aufgelöst“.
In der Praxis erweist sich damit die gängige Faustregel „Maximale Blende gleich zweimal Pixelgröße in Mikrometern“ als um mindestens 1–2 Blendenstufen zu pessimistisch.
Das Thema ist also weitaus komplexer, als es hier darstellbar ist. Wenn der Text jedoch ein bisschen zum Verständnis der Grenzen der Auflösung beigetragen hat und zeigen konnte, das diese Grenzen weiter gesteckt sind, als gemeinhin angenommen, so ist das Ziel erreicht.
Zu guter Letzt …
… bleibt noch anzumerken, dass sich unsere Betrachtungen darauf bezogen, dass wir ein perfektes Objektiv haben, das keinerlei Abbildungsfehler aufweist, das es in der Praxis so eigentlich nicht gibt. Wie gesagt: „eigentlich“. Die modernen Optikschmieden sind heute jedoch durchaus in der Lage, Optiken (und dabei denke ich jetzt auch an Spiegeloptiken) zu bauen, bei denen die Abbildungsfehler der „Linse“ gegenüber der Beugungsgrenze vernachlässigbar sind. Die Auflösung der Optik kann also gegebenenfalls nicht durch irgendwelche Fehler in den Abbildungseigenschaften der Optik begrenzt sein, sondern erst durch die Beugung, wie hier dargestellt. Oder, anders ausgedrückt: Perfekte Optiken, nur begrenzt durch die Beugung, existieren tatsächlich.
(Randolf Butzbach)
R.B. ist promovierter Physiker und hat sich u.a. mit den Grenzen der Auflösung von Optiken für Röntgenstrahlen beschäftigt. Privat fotografiert er seit seinem 10. Lebensjahr.
Mit Dank an Hubert H. Nasse, Carl Zeiss AG, für die Durchsicht und wertvolle Anregungen.
Zum Weiterlesen:
Wie liest man MTF-Kurven? (PDF-Datei)
Wie liest man MTF-Kurven? – Teil II (PDF-Datei)



Danke!
Endlich ein fundierter, niveauvoller Beitrag zum Thema!
Didaktisch hervorragend und für jeden, der einmal Physik gelernt hat, nachvollziehbar.
An die Photoscala-Redaktion: bitte mehr davon!
Dem schliesse ich mich an.
Dem schliesse ich mich an. Danke für den fundierten und nachvollziehbaren Beitrag, der die früheren Artikel von Hr. Nasse zum gleichen Thema sehr schön ergänzt.
Sehr wohl verstanden!
[quote=Gast]Fotografieren ist das was ein jeder -für sich- daraus macht.[/quote]
Ja. Und man kann was Kreatives machen oder einfach nur palavern! Eine sehr kluge Frau hat mal gesagt, dass jeder sich möglichst als GESTALTENDES Mitglied der Gesellschaft zu betätigen versuchen sollte. Das bezog sich zwar auch auf andere Lebensbereiche, aber das sollte auch für die Fotografie gelten. Die ist nämlich in erster Linie eine Kunst – und Kunst lebt von Kreativität. Indem man über Auflösungsgrenzen etc. schwadroniert, schafft man rein gar nichts. Außer vielleicht viel heiße Luft. Die Zeit, die man mit solchen Fachsimpeleien verplempert und/oder mit dem Lesen solcher Artikel verbringt, wäre besser darin investiert, sich seine Kamera zu greifen und auf Motivjagd zu gehen! Oder zumindest sich mit den praktischen Aspekten der Fotografie auseinander zu setzen d.h. neue Techniken in der Praxis auszuprobieren. Denn bei solchen Diskussionen ist man zwar im Nachhinein um Einiges schlauer bzw. an reiner Theorie reicher, aber es fehlt ein greifbares Resultat. In dem man aber ein Bild schafft, gewinnt man nicht nur an – deutlich wertvollerer – praktischer Erfahrung, sondern hat auch was Konkretes vorzuzeigen. Und wenn es ein gutes Bild ist, sogar etwas was man mit anderen Menschen (auch technisch Unversierte) teilen kann. Ein Bild ist da, um was (z.B. Emotionen) mit anderen Menschen zu teilen und manchmal sogar um die Kultur voran zu bringen; DAS ist deutlich mehr wert als jede noch so fundierte technisch-wissenschaftliche Diskussion!!!
Wow!
Was für ein fundierter Beitrag! Offensichtlich hängt in der Digitalfotografie vieles mit Allem irgendwie zusammen. Es gibt die Physik, aber es gibt auch die Digitaltechnik. Wenn ich viele Megapixel habe, die optische Systeme an die Grenzen bringen, dann kann ich immer noch runterrechnen und das Bild ist trotzdem gerettet. Trotzdem bin ich der Meinung, das 24 Mpx bei Vollvormat eine gute Grüße sind. Hoffen wir, das die neu avisierte Sony a99 nicht dem Nikon d800 Beispiel folgt!
Gast schrieb:
theoretisch
[quote=Gast]theoretisch wie praktisch falsch.[/quote]
Oh. Ein Auskenner! Kommt gleicht eine VF-Orgie?
Der Spaniel. Wau!
Außerdem bilden die
Außerdem bilden die modifizierten Gauß-Objektiv-Typen eine hervorragende Bildfeldebnung mit bester Detailschärfe ab und sind für hohe Öffnungsverhältnisse oft optimal auskorrigiert.
Das Summicron M 2/35mm plus RVP100F bleibt mein Favorit für farbige Erinnerungsfotos auf Reisen und von meiner Familie – nach meinen ersten Erfahrungen mit den Laborabzügen von CCD/CMOS DSLR Bilddateien plane ich meine SW-Dunkelkammer (Silberhalogenid Negative & Positive) zu reaktivieren (KB/MF-Filme, Entwickler etc warten schon gut gekühlt zur weiteren Verwendung) …
Der Spanier. Viva. schrieb:
[quote=Der Spanier. Viva.]Die neuen Objektive und ‘Kit’-Objektive nenne ich schon seit Jahren bottle bottom glasses (Pressglas-Flaschenbodengläser). Die werden ‘auf Kante’ gerechnet, billigst produziert und die Fehler per Software korrigiert.
Einfach mal ein paar ZEISS (35mm), Rodenstock (GF), Schneider (MF & GF), Fuji (MF & GF) oder alte Nikon-Objektive (35 mm & GF) mit dem neuzeitlichen Krempel vergleichen, dann wird sehr schnell klar, welcher Murks heutzutage für zu viel Geld in den Markt gedrückt wird.[/quote]
Und gleich erklärst Du uns bestimmt, daß Du anhand der Aufnahme das verwendete Objektiv erkennen kannst, gelle? Also der Pepsi-Cola-Test für Flaschenbödenexperten; bitte erzähle uns nochmal den Teil des Märchens, wie man Objektive “auf Kante” rechnet. 😉
Der Spaniel. Wau!
P.S.: Woher kommt Deine Sachkentnis der “Pressglas-Flaschenbodengläser”? Zu viel San Miguel?
Also da bleibt nur
ungeschaut festzustellen: Sie sehen in Wirklichkeit gar nix.
Und nebstbei: Beugungsgrenzen richten sich nicht nach der ART des Sensors, sondern allein nach seiner Pixeldichte. Der Physik ist CCD oder CMOS quasi sch…egal, da geht’s ganz einfach um Maß und Zahl.
Ein Zuviel
ist allerspätestens dann erreicht, wenn ich die Pixel so klein mache, dass grad noch je ein Photon darin Platz findet … ganz theoretisch betrachtet, versteht sich. 😎
Als Witz
taugt’s für manchen Verstand auch sicher nicht … 😎
Verrannt
und vernebelt – fern jeglicher Praxis, die den eigentlichen Maßstab bildet.
Wie Sie dem
zur Diskussion stehenden Beitrag entnehmen können, ist die Photonenanzahl je Pixel eine wohldefinierbare Größe – die auch keineswegs unterschritten werden sollte, um 1. eine brauchbare Information bei 2. einem vernünftigen Dynamikumfang zu erhalten.
Winzig klein
ist eigentlich keine Beschreibungsgrundlage für ein masseloses Elementarteilchen wie das Photon. Eher schon Energie in Wechselwirkung in einem umgebenden Medium, wir bewegen uns hier auf der Ebene der Quantenphysik. Photonen sind Bosone, so wie das Higgs-Boson.
Die entstehen…
…bei der Aufnahme bedingt dadurch, das die RGB-Farbkanäle nicht gleichzeitig in die Sättigung gehen. Somit ergeben sich gem. RGB-Mischung eben beliebige Farbtöne.
Wenn Sie das von Ihrer Kamera her nicht kennen, dann haben Sie keine D3X oder andere Kameras mit harter Kennlinie und eingeschränktem Dynamik-Umfang. Die D3 hat z.B. eine weiche Kennlinie in Lichtern und ist eigentlich als Kamera mit Consumer-Sensor-Kennlinie zu bezeichnen. Weiche Kennlinie in Lichtern wird allerdings auch von Reportage-Fotografen begrüßt. Wer mag schon Farbkringel um Spitzlichter? Der Dynamikumfang ist dann aber getürkt und v.a. verschütten die Ladungsspeicher des Pixels schlichtweg “Information”. Das darf man nicht mit weicher Kennlinie in Lichtern beim Farbnegativ-Film vergleichen.
Information =
0 oder 1 und damit wird man nicht viel erkennen. Das als “erstens”.
Als “zweitens” gilt, dass soweit nur 1 Photon noch reinpaßt man sich um die Aufenthaltsorte der Ladungsträger Gedanken machen muss und die sind nunmal größer, wenn man aus Ladung/elektron einen Spannungswert erzeugen möchte.
Wahrscheinlich so
wie jede andere Digitalkamera, deren Nennempfindlichkeit 100 ASA beträgt … 😉
Lassen Sie’s
Für blöde Witze sind Sie viel zu gescheit … 😎
Witz ist relativ
Ich fand’s zumindest, auch eingedenk des Autors, als nicht wirklich Ernst gemeint. Niemand denkt ernsthaft an einen Sensor, dessen Pixel grad mal ein Photon verarbeiten könnten. Außer Ihnen, der sich zwangsneurotisch zur Aufklärung drängt.
Danke für Ihre Frage …
… eigentlich wollte ich auf Motive mit sehr hohen Kontrasten hinweisen, die auch in unseren Breiten – beispielsweise bei sonnigen Strandszenen (im Urlaub) – häufig vorkommen …
sri
Auch danke
Bestätigt aber auch wieder mal die Lebensweisheit, dass zu wenig und zu viel der Narren Ziel ist.
Warum?
Warum so viel Selbstkritik? [quote=Gast]Bestätigt aber auch wieder mal die Lebensweisheit, dass zu wenig und zu viel der Narren Ziel ist.[/quote]
Ohne falsche Bescheidenheit
[quote=Gast]Nicht alles, was man nicht versteht, ist deshalb überflüssig.[/quote]
Jeder der weiß, welche Person hinter dem Pseudonym DingDongDilli steckt, dürfte wissen dass es mir an Fachwissen nicht fehlt und ich durchaus in der Lage bin, den obigen Artikel zu verstehen…
Nicht die Beugung wird begrenzt
Die Beugung begrenzt.
Ich zitiere
s.o.:
…
Gilt also doch: Je größer die Pixel desto größer das Signal-Rauschverhältnis?
Auch hier haben wir wieder ein Ja-Aber: Denn je größer die Pixel werden, desto empfindlicher wird zwar das einzelne Pixel für das Licht (wie gewollt), aber gleichzeitig wird es auch (ungewollt) empfindlicher für Störeinflüsse wie z.B. Wärme. Das Signal-Rauschverhältnis verbessert sich also irgendwann nicht mehr. Das Einzige, was hilft, ist durch ein intelligentes Schaltungsdesign das Ausleserauschen möglichst gering zu halten und den Wärmeanteil aufwendig durch Kühlung zu reduzieren – wobei letzteres in einer Kamera selten praktikabel ist.
…
…
Wie man leicht sieht, zählt dabei das Verhältnis vom gewollten Signal zum sogenannte Helligkeitsrauschen, also der Belichtung des Pixels unter anderem durch Wärme (der Sensor ist nicht nur für sichtbares Licht empfindlich!), der statistischen Streuung der einfallenden Photonen und damit der erzeugten Elektronen (bei identischer Belichtung!), sowie von der Belichtungszeit unabhängige Störungen, die durch das Auslesen entstehen.
Um mal Butter bei die Fische zu geben, ein konkretes Beispiel: Der Kodak KAF-40000 Fullframe-CCD-Sensor, dessen Spezifikationen sich sehr gut mit denen der Pentax 645D decken, hat laut Datenblatt (PDF-Datei) eine Kapazität von 42.000 Elektronen pro Pixel. Der Rauschuntergrund besteht dagegen aus 13 Elektronen Ausleserauschen, was ein Signal-Rausch-Verhältnis von 42.000:13 oder 3231:1 ergibt. Hinzu kommt (bei 60° C Sensortemperatur) die wärmebedingte „Belichtung“ von 42 pA/cm2, d.h. 262 Millionen Elektronen pro Sekunde und Quadratzentimeter bzw., bei einer Pixelgröße von 6×6 µm2, 94 Elektronen pro Sekunde und Pixel. Dieser Wert verdoppelt sich alle 5,5° C: Bei 65,5° C sind es also schon 188 Elektronen/Sekunde, bei 71°C 376 Elektronen, usw. Bei einer angenommenen „Belichtungszeit“ von einer 1/50 Sekunde (also der Zeit zwischen letzten Löschen und Auslesen) ergäbe sich so bei 60°C Betriebstemperatur ein Wärmeanteil von ungefähr 2 Elektronen/Pixel. Zusammengenommen bedeutet das ein Signal-Rausch-Verhältnis von 42.000:(13+2) oder 2800:1. Damit hätten wir einen Dynamikumfang von 2800:1 oder 11,5 Blendenstufen, wie Kodak und Pentax ihn in den Technischen Daten kommunizieren.
…
…
Mit dem Erscheinen der Nikon D800/E mit ihren 36 Megapixeln auf Leica-Format (vulgo: Kleinbild, Vollformat, FX), der Sony Alpha 77 mit 24 Megapixeln auf APS-C, der Sony RX100 mit ihren 20 Megapixeln auf 1-Zoll-Sensor, oder dem Handy Nokia 808 mit fast 42 Megapixeln ist die Diskussion um die Grenzen der Auflösung voll entflammt:
…
+++++++++++++++++Zitate ende+++++++++++
Wer Anfangs von CMOS-Kameras schreibt und “Ja-Aber”, etc. mit CCD-Beispielen verargumentiert, hierbei das deutlich geringere Rauschverhalten beim Auslesen von CMOS übersieht war etvl. bei Beugungserscheinungen und Kontrasteffekten gut unterwegs aber beim Ausleserauschen fachlich daneben.
Beim CCD ist es Ladungstransport(-Auslese)-Rauschen und beim CMOS wohl eher Störsignaleinkopplungen durch rauschende Schaltkreise aus dem Substrat. Das ist kein Rauschen, dass nur im Moment der Abfrage der Pixelwertinformation entsteht. Man sollte das anders nennen als das Ausleserauschen beim CCD-Typ.
So einfach ist das.
Desweiteren lese ich nichts über die Beiträge des LowPass-Filters bzgl. der Beugungsgrenze bedingt durch den Pixelpitch/Pixelabstand. Wahrscheinlich kann man einen LowPass-Filter applizieren, welcher die theoretische Auflösung des Sensors gar halbiert bzw. noch besser viertelt und immer noch glauben die meisten Leser hier, dass nur der Pixelpitch relevant ist.
Zuletzt: LowPass-Filter, Bayer-Pattern-Farblayer und Microlinsen und die seitlich die Microlinsen umfaßenden Schaltungsschichten sind ebenfalls Orte mit Beugungserscheinungen und v.a. einen Effekt, welcher die tatsächlich von der Objektiv-Blende projezierten Beugungsmuster verschleift und sichtbar sogar verrauscht. Das ist das Pixel-Cross-Talking.
Und dann käme noch Chromatische Abberationen in den Microlinsen dazu.
Und wenn die optische Schnittstelle eben optisch nicht optimal funktioniert, dann kann einem die blanke Physik der Beugung an der Objektiv-Blende und bedingt durch den Pixelpitch im Grenzfall “wurst” sein, dann sieht man nah an der Beugungsgrenze ganz andere unschöne Artefakte wie nur weniger lp/mm als im Optimalen Arbeitsblenden-Bereich.
Dann bändigen…
..Sie mal die farbigen Kringel um Spitzlichter bei Aufnahmen mit einer Nikon D3X. Und zwar die Spitzlicht-Reflexionen an Augen. Nicht belichtungstechnisch vermeiden sondern damit Belichtungseinstellungsmäßig umgehen. Ihnen reichen weder die 12 EV Dynamikumfang des D3X-Sensors aus noch die 14-Bit-RGB-Signalverarbeitung der D3X, denn der CMOS der D3X besitzt in Lichtern einer harte Kennlinie.
Dann doch zu consumerlike Sensoren greifen wie CMOS mit künstlich weich gemachter Kennlinie in Lichtern.
Es geht auch anders. Siehe FFT CCD allgm. und CCD von Kodak mit Astronomie-Fotografie-Spec., zB. CCD der Olympus E-400. Letzterer verbrennt hell-geblich wie Farbnegativ-Film und darf bei Sternenlichtern keine Fehlfarbenen Kringel um Spitzlichter/Sternlichter zeichnen.
Bei CMOS scheint das nur die NASA (dort wurde der CMOS-Typ erfunden) hinzu bekommen. Dafür ist dann die Aufnahme v.a. technische Fotografie aber keine Imaging-Fotografie.
Kinderschuh-Thema diese Digitalfotografie. Da wird jeder Artikel gleich als fachlich super angesehen solange er sich in populären Gefielden aufhält und v.a. eines nicht tut: Zuviel Staub aufwirbeln.
Es wird noch viel Staub aufgewirbelt werden.
Dann…
…machen Sie bitte jetzt noch den nächsten Schritt und erklären wie klein oder große ein Pixel sein muss, damit 1 Photon grad noch so reinpaßt. Dann als nächstes warum es dann Probleme mit der Funktionsweise des Pixel-Arrays gibt, wenn man nicht darauf achtet, dass z.B. beim CMOS-Sensor Ladung also das oder die vom Photon oder von den Photonen ausgeschlagenen Elektronen die Chance haben in einem Ladungstrog gespeichert zu werden bevor der Ladungwert in einen Spannungswert gewandelt wird. Und das direkt am Pixel. CCD funktioniert etwas anders. Hier würden bei einen Single-Photon-16MPx-Sensor pro Pixel 1 Elektron abzutransportieren sein. Pro Ladungsschiene die Pixelwertzahl gem. Bildhöhe und in Summe eben die effektive Pixelzahl. Das sind ca. 16 Mio. Elektronen. Das alles reicht, wenn man das quasi Pi-mal-daumen durchrechnet. So nun walte Deines Amtes.
Ansonsten, so als Tipp. Die Bemerkung so wie Sie bisher im Raum steht wäre nämlich so als würde man jemanden erklären warum er jemanden das Photon aufs Papier zeichnet und als Teilchen/Particle darstellt um etwas “vereinfacht”/”abstrahiert” zu erklären bzw. wie in diesem Fall “Vor Augen zu halten”. Desweiteren dürfte zumindestens dem Boson-Insider aufgefallen sein, dass die Wellenlänge bestimmt wo das Photon so eindringt, dass es in einer Arraystruktur wie beim Sensor auch quasi ins Loch trifft. Oder wollen Sie einen wahllos(randomly) Bildpunkt-Informations-verschleifenden Sensor konstruieren? Einfaches Beispiel: eine Pixelreihe soll lauter 1 (1 elektron) als Info abspeicher gem. Bildvorlage. Nun ergibt sich wg. Pixelraster ungeeignet für die Wellenlänge der Photonen, dass das ein oder andere z.B. ganz woanders quasi beim Nachbarn einschlägt. Soweit 2 reinpassen haben wir Zahlücken mit immer wieder spitzen Zähnen. Da soweit zur Physik und das bildhaft erklärt. Auch das Borsche Atommodel ist im Vergleich zum genaueren Model incl. Elektronen-Wolken nicht ohne Kritik aber man muss sich immer wieder fragen was Ziel der Vereinfachung war oder ist.
Unterm Strich aber gilt eben. Nur was der Mensch technisch so beherrscht, dass er es massenweise reproduzieren kann ist nicht zu klein was die Strukturgrößen betrifft.
Ja und aber
Die Betrachtung in Foren ergeht sich halt nicht in der (unbestrittenen) Theorie, sondern in der täglichen, oft langjährigen Praxis. Und die ist in der Regel nicht von allein
beugungsbegrenzten Optiken, und auch nicht immer von hohen Lichtstärken geprägt. Und da hier, richtiger Weise, auf ein Maximum an Auflösung UND Dynamikumfang verwiesen wird, werden wir uns auch weiterhin nach bestmöglichen Kompromissen aus Auflösung, Dynamik und, natürlich, möglichst guten Optiken umschauen müssen.
Aber nur
[quote=Gast][quote=Gast]was sagt uns da jetzt für die Praxis ?[/quote]
Daß es kein “zu viel” an Sensorauflösung gibt, entgegen der gängigen Forenmeinung.[/quote]
wenn man sich fälschlicher Weise allein auf die Auflösung fokussiert. Was aber noch nicht mal der Autor tut … 😎
ein Zuviel
gibt es nur für die Leute, die immer den neuesten Quark von irgendwas haben müssen und dann feststellen, dass sie für viel Geld zu früh gekauft haben, obwohl eigentlich feststehen müsste, dass der Verkauf ähnlich wie früher bei den Computern funktioniert: mehr und noch besser immer erst später.
Und jetzt muss es doch irgendwie gelingen, den “Fortschritt” tot zu quasseln. Gelingt zwar nicht, weil halbwegs aufmerksame Zeitgenossen sich sehr schnell ein Bild machen, was da wirklich Sache ist. Blöd gelaufen.
Gurus.
Aha. Soso. Gurus. Pixelwertgüte. Schamanen. Farbgüte. Medizinmänner. Pixel-Interpolation. Voodoo. Parapsychologie. Im Rauschverhalten eben deutlich besser für Reportage-Fotografen geeignet.
Alles klar.
Aha, Mr. FT gibt sich mal wieder die Ehre!
FFT-CCDs sind und werden vermutlich auch in der Zukunft exotische Sensoren bleiben, auch wenn es da sicher den einen oder anderen Vorteil gibt. Aufs Ganze gesehen, sind die Nachteile für die Mehrzahl der Anwender aber doch überwiegend.
Dagegen steht das Design des 1″ Sensors von SONY, das erkennbar in der Breite Qualität anbietet zu brauchbaren Kosten und für eine Menge Anwendungen. Das ist es, was der Markt im wesentlichen Teilen nachfrägt.
Gast schrieb:
Was dem
[quote=Gast]Was dem Artikel jedoch fehlt ist Active Pixel Sensor-Know-How, denn der hat im Vergleich zum CCD-Typ kein Ausleserauschen. [/quote]
Das wäre schön, aber so einfach ist es leider nicht.
“Faszinierend”
würde Mr. Spock sagen.
vielen
dank!
Und Thomas Maschke hat doch recht
Dem kompetenten und sehr differenzierten Beitrag von Randolf Butzbach ist im Einzelnen nicht zu widersprechen. Danke für die fundierte Betrachtung. Allerdings ist die Schlußfolgerung nicht ganz schlüssig.
Die im Beitrag herausgearbeiteten minimalen Kontrastunterschiede sind nämlich für die Bildwirkung irrelevant. Das war schon so bei Agfa-Ortho 25 mit “weichem” Doku-Spezialentwickler (z.B: Neofin Doku). Das Auszählen von gerade noch wahrzunehmenden Gittermustern konnte mehrere 100 Linien/mm bringen ohne dass die Bilder besonders scharf wirkten, das war nur Auflösung ohne Mikrokontrast.
Daher hat sich die Beurteilung mittels der MFT (Modultions-Transfer-Funktion) eingebürgert. MFT50 ist der übliche Bewertungs-Standard von Objektiv-Kamera-Kombinationen. Sie gibt an, bei wieviel schwarz-weissen Linienpaaren/mm noch einen Kontrast von 50% erhalten bleibt.
Im Beitrag von Randolf Butzbach ist eine sehr gute Darstellung der MTF-Kurven für verschiedene Blenden aufgetragen. Bei Blende 4 werden gerade mal 200 Linienpaare mit 50% Kontrast aufgelöst, bei Blende 2 sind es 400. Nimm mann zunächst an, dass für ein Linienpaar immer zwei Pixel längs einer Zeile zuständig sind, kommt man bei Blende 4 auf 100 Pixel pro mm, also 10µm Pixelgröße, bei Blende 2 auf 200 Pixel pro mm, also 5µm Pixelgröße. Für einen APS-C Sensor mit 14,8 x 22,2 mm kommt man bei Blende 4 auf 3,3 Mpx bei Blende2 auf 13 Mpx. Das wäre bei pei puristischer Betrachtung des MTF50-Kriteriums die untere Grenze für Pixelgröße und Megapixel-Zahl bei APS-C.
Zur Vermeidung des Moiré-Effektes bei periodischen Strukturen ist vor digitalen Sensoren ein Licht streuendes Antialiasing-Filter erforderlich. Es reduziert den Moiré-Effekt auf Kosten des Mikrokontrastes. Daher verwendet man feinere Sensorpixel und feinere Antializing-Filter. Im Übrigen werden durch diese Übertastung, wie im Beitrag von Randolf Butzbach sehr schön gezeigt und abgebildet, die feinen Strukturen im Beugungsbereich differenzierter wiedergegeben.
Also die Formeln von Thomas Maschke stimmen schon. Es gibt aber andere Gründe, z.B. Moiré, und differenzierte Feinststruktur, die eine höhere Pixelzahl als vorteilhafter erscheinen lassen. Übrigens wird dabei das Rauschen wird kaum höher, wenn man auf gleiche Pixelzahl runterrechnet. Letzteres gilt aber erst seit der Einführung der rückwärtig belichteten Sensoren (BSI), die keinen Flächenverlust durch notwendige elektrische Leitungen und Transistoren haben.
Genau das ist das übliche Mis(t)verständnis der MTF
[quote=Gast]Daher hat sich die Beurteilung mittels der MFT (Modultions-Transfer-Funktion) eingebürgert. MFT50 ist der übliche Bewertungs-Standard von Objektiv-Kamera-Kombinationen. [/quote]
Es ist zu unterscheiden zwischen den von Objektivherstellen angewendeten MTF-Kurven, wie sie im oben verlinkten Artikel von Hr. Nasse beschrieben sind, und den wenig aussagekräftigen 50% Kurven à la photozone. Letztere sind zur Beschreibung des Bildeindrucks wenig geeignet, wie auch in den verlinkten Artikeln von Hr. Nasse dargestellt und mit Bilder eindrucksvoll belegt ist.
Die MTF50 von photozone usw. sind der Versuch, den Bildeindruck in eine einzige Zahl zu packen, die einfach messbar und für Laien überschaubar ist. Wirklich aussagekräftig ist sie aber nicht. Wesentlich geeigneter sind “echte” MTF-Kurven mit MTF bei 10, 20, 40 Lp/mm. Die zu lesen erfordert aber ein wenig Übung. Wenn man’s verstanden hat, dann wird man mit wirklich aussagekräftigen Daten belohnt, die auch den Bildeindruck korrekt beschreiben.
Leider basiert dein Kommentar auf genau dem beliebten, über-vereinfachten Model, daß auch der MTF50 Messung zugrunde liegt. Der obige Artikel zeigt, warum das so eben nicht stimmt.
Genau diese Erfahrung habe ich auch gemacht!
[quote=Gast]Übrigens wird dabei das Rauschen kaum höher, wenn man auf gleiche Pixelzahl runterrechnet. Letzteres gilt aber erst seit der Einführung der rückwärtig belichteten Sensoren (BSI), die keinen Flächenverlust durch notwendige elektrische Leitungen und Transistoren haben.[/quote]
Meine D90 kackt regelmäßig gegen das Auflösungsvermögen einer Coolpix S8200 ab. Die Detailzeichnung ist so man die S8200 gekonnt einsetzt teils schon fast grandios! Voraussetzung ist das man die 16MP auf 8MP herunterrechnet! Ist jetzt die D90 schlechter? Nein der Auflösungsvorteil der S8200 hat seine Grenzen und ist für den Alltag nicht so relevant. Es sei denn man zeigt ausgesuchte Bilder der Cams parallel. Aber wie schon geschrieben trifft das nur auf die rückwärtig belichteten Sensoren zu, da diese ca 40% mehr Licht zur Auswertung auf die Pixel bekommen. Die Aussage weniger ist mehr stimmt in diesem Fall seit dem nicht mehr!
Hab’ was gelernt
das ich gar nicht wissen wollte und mit dem ich auch nichts weiter anfangen kann.
Purer Luxus, finde ich gut.
Zurück in die Zukunft
Fotografie ist KEINE Wissenschaft!
So fundiert der Artikel auch sein mag, ist er IMO so überflüssig wie ein Kropf, da es bei der Fotografie NICHT darum geht, die technische Perfektion zu erreichen bzw. das perfekteste Objektiv zu besitzen, sondern das beste Auge fürs schöne Motiv zu haben, die besten Bildideen zu entwickeln, letztere auf die bestmöglichste Weise umzusetzen usw.. Alles Fähigkeiten, die man definitiv nicht entwickelt indem man über Auflösungsgrenzen und sonstige technische Limitationen fachsimpelt…
Genau.
da hat DDD mal Recht.
Und wer alle teuren Linien(paare) der ganzen Objektive, die er sich auf Grund durchaus qualifizierter und ernstzunehmender Test vielleicht kauft, ausnutzen will, darf nur noch vom fest einbetonierten Stativ fotografieren.
Ich warte noch auf den Test, der uns sagt, wieviel Prozent der ganzen schönen teuer bezahlten Linien(paare) pro mm sich in nichts auflösen, sobald aus freier Hand fotografiert wird.
Zum Glück kommt es in Wirklichkeit bei dem, was gelungene Fotos ausmacht, auf ganz was anderes an.
Für alle die mehr wissen wollen, hier ein ganz heisser Tip – bringt praktisch mehr als 1000 Tests und Beiträge wie dieser auf Photoscala, und mögen sie auch noch fundiert sein:
http://www.fotofeinkost-verlag.de/wie-man-ein-grossartiger-fotograf-wird/
Pressestimmen: http://www.fotofeinkost-verlag.de/wie-man-ein-grossartiger-fotograf-wird/pressestimmen
(leider zur Zeit vergriffen)
Zugegeben: mit gutem Werkzeug macht Fotografieren mehr Spaß. Aber für die besseren Fotos bleibt der Fotograf und nicht der Ingenieur zuständig.
“Man kann nicht beides sein,
Realist und dann auch noch beliebt.”
Falsch verstanden!
Fotografieren ist das was ein jeder -für sich- daraus macht. Manche verdienen damit Geld, einige haben einfach Freude daran oder andere wie im Beitrag hier betrachten das alles ganz nüchtern wissenschaftlich. Diese unterschiedlichen Aspekte der Fotografie und Ansprüche macht die Sache ja erst richtig interessant. Zumindest für mich.
OJe
Nicht alles, was man nicht
Nicht alles, was man nicht versteht, ist deshalb überflüssig.
Naja…
…Anreize für Artikel wie diese muss es geben anstatt eigentliches Interesse oder Nutzen. Der Nutzen wird meist spät erkannt und dann Interesse geweckt.
Anreiz für diesen Artikel wurde klar formuliert: z.B. Nokia 808 PureView mit 41 MPx.
Was dem Artikel jedoch fehlt ist Active Pixel Sensor-Know-How, denn der hat im Vergleich zum CCD-Typ kein Ausleserauschen. Im Artikel wird über Ausleserauschen gesprochen. Das ist für Leica M9 FFT CCD vs. digitales Mittelformat FFT CCD relevant aber für genannte Nikon D800 mit CMOS nicht. Durch die hohen Framerates kommt es allerdings zur Erwärmung nötiger Schaltkreise und die Wärme erhöht die Störladungsrate auf der CMOS-Oberfläche incl. Pixelfläche. D.h. CMOS-Thema ist thermischen Rauschen bzw. Halbleiter-Oberflächen-Störladungen. Der Pixelwert wird am Pixel erzeugt und dann wird der Spannungs-/Pixel-Wert kaum noch von Leitungsbahn-Rauschen gestört.
Und wenn wir schon gerade dabei sind. Integriert Bildstabilisierung durch bewegliche Sensormodule erfordern eine entsprechend gute Wärmeableitung. Zwischen Sony SLT und Sony NEX gab es anfangs klare Unterschiede bei der Abschaltzeit bei Videoaufnahmen.
Desweiteren fehlt mir die Betrachtung von Pixel-Cross-Talking, etc.. Wenn schon das Nokia 808 PureView ein Anreiz war sollte man sich auch mit den Ansätzen und Techniken gem. OpenCamera-Project beschäftigen, denn aus dieser Kooperation mit ein US-amerikanischen Uni zieht Nokia sein Know-How sowohl für Non-realtime Interpolation per Multi-Framing (s. BlessN900 für Nokia N900) und Pixel-Interpolation wie beim 808 PureView.
Meiner Meinung nach sollte man sich mal an niederländische und kanadische Experten von DALSA wenden. Die Niederländer sind CCD-Gurus und die Kanadier CMOS-Gurus.
Die Eindhovener Truppe kann auch erklären warum deren FFT CCDs vertikale Ladungsüberschuss-Drainagen haben, während Kodak FFT CCD bei den Ladungsdrainagen in die Fläche geht, d.h. diese in horizontaler Lage ausführt. Beeinflusst nämlich nicht nur den Füllgrad des Sensors sondern auch Microlinsen-Design bis hin zur Möglichkeit ganz ohne Microlinsen auszukommen. Wie man sicherlich bestätigen wird sind die Microlinsen bzgl. sichtbaren Beugungserscheinung mit von Bedeutung. Allerdings auch von Bedeutung beim Pixel-Cross-Talking.
Fototechnik ist eine Wissenschaft und die DALSA-Mannschaft besteht u.a. aus den dafür nötigen Gurus. Der ein oder andere ist sicherlich privat ein Fotograf.
Es gibt aktuell einen Umbruch bzw. 2 Wege
1. Optisch optimierter Sensor nach CCD-Vorbild nur eben rauschfreier wie CCD und im Rauschverhalten eben deutlich besser für Reportage-Fotografen geeignet.
2. Interpolation von Pixelwerten um bei der Pixelwertgüte und va. Farbgüte besser dazustehen wie bisher. Dies jedoch zur Verwunderung vieler (?) haarscharf an der Beugungsgrenze.
Der Mensch ist von Natur aus neugierig. Der Anreiz für genauere Untersuchungen ist schlichtweg da…
Na sowas,
[quote]liegen diejenigen, die mit ihren MicroFourThirds- oder gar Kompakt-Kameras, die ein sehr feines Pixelraster haben (vgl. Tab. 1), überraschenderweise brauchbare Bilder erhalten – was gemäß der weit verbreiteten Meinung zum Thema Auflösung eigentlich undenkbar ist.[/quote]
das ist ja glatt Störfeuer für das übliche Deppenkonzert, das man sonst immer hört. Was wir Anwender von solchen untauglichem Gerät ohne theoretischen Überbau schon immer aus der Praxis wissen, jetzt sozusagen wissenschaftlich bestätigt.
Ich frage mich sowieso, wie das mit den Mikrokameras von früher, die man durchaus für alle möglichen Dokumentationsaufgaben, sprich Spionage, verwendet hat, gegangen ist. Das war wahrscheinlich alles Hokus-Pokus. Aber egal. Leute, die sich aus guten Gründen mit kleinen Kameras herumschlagen, wissen schon lange, dass diese Kameras durchaus in der Lage sind, hervorragende Leistungen zu bringen, wenn man sich mit dem Potential der Kameras über die Standardeinstellungen hinaus auseinandersetzt.
Geradezu witzhaft empfinde ich immer diese Spezialisten, die einerseits den hohen ISOs das hohe Wort reden und gleichzeitig das ewige Mantra von der Beugungsunschärfe bei angeblich zu hoher Auflösung daherbeten (egal wie immer das aussieht). Als wäre das nicht schon ein geradezu definierter Widerspruch in sich. Allein was da an Rauschen und sonstigen Störungen an “Schärfe” versemmelt wird, unglaublich.
Entscheidend ist: Auflösung schafft Reserven und ist deshalb schlicht durch nichts zu ersetzten. Punkt.
Die sieht so aus
dass sich das Auflösungsvermögen – die Detailwiedergabe – halt sichtbar reduziert. Ganz unabhängig davon, wie sehr man sie schon allein dadurch reduziert, wenn man nicht vom Stativ aus fotografiert. Noch drastischer formuliert: Du fotografierst mit einer 24 MP-Cam, und kriegst Ergebnisse, wie aus deiner verflossenen 6 MP-Cam. Aber richtig ist auch: Das hat nichts mit der inhaltlichen Qualität von Bildern zu tun. Es ist nur, bei manchen Motiven, ärgerlich – aber, mit dem entsprechenden Knowhow, vermeidbar.
Messerscharf
[quote=Gast][quote]liegen diejenigen, die mit ihren MicroFourThirds- oder gar Kompakt-Kameras, die ein sehr feines Pixelraster haben (vgl. Tab. 1), überraschenderweise brauchbare Bilder erhalten – was gemäß der weit verbreiteten Meinung zum Thema Auflösung eigentlich undenkbar ist.[/quote]
das ist ja glatt Störfeuer für das übliche Deppenkonzert, das man sonst immer hört. Was wir Anwender von solchen untauglichem Gerät ohne theoretischen Überbau schon immer aus der Praxis wissen, jetzt sozusagen wissenschaftlich bestätigt.
Ich frage mich sowieso, wie das mit den Mikrokameras von früher, die man durchaus für alle möglichen Dokumentationsaufgaben, sprich Spionage, verwendet hat, gegangen ist. Das war wahrscheinlich alles Hokus-Pokus. Aber egal. Leute, die sich aus guten Gründen mit kleinen Kameras herumschlagen, wissen schon lange, dass diese Kameras durchaus in der Lage sind, hervorragende Leistungen zu bringen, wenn man sich mit dem Potential der Kameras über die Standardeinstellungen hinaus auseinandersetzt.
Geradezu witzhaft empfinde ich immer diese Spezialisten, die einerseits den hohen ISOs das hohe Wort reden und gleichzeitig das ewige Mantra von der Beugungsunschärfe bei angeblich zu hoher Auflösung daherbeten (egal wie immer das aussieht). Als wäre das nicht schon ein geradezu definierter Widerspruch in sich. Allein was da an Rauschen und sonstigen Störungen an “Schärfe” versemmelt wird, unglaublich.
Entscheidend ist: Auflösung schafft Reserven und ist deshalb schlicht durch nichts zu ersetzten. Punkt.[/quote]
falsch geschlossen – weil offensichtlich ungenau gelesen.
Klasse Artikel
Mehr in der Art bitte.
OhWeh
Jetzt habe ich das
Jetzt habe ich das Higgs-Boson endlich verstanden!
Na
[quote=Gast]Jetzt habe ich das Higgs-Boson endlich verstanden![/quote]
hoffentlich haben Sie nicht erst jetzt verstanden, dass Materie nicht aus dem aufgebaut ist, was entsteht, wenn man Materie zerdeppert (Glas besteht ja im Wesentlichen auch nicht aus den Scherben, die beim Fallenlassen entstehen) … 😎
Und
was sagt uns da jetzt für die Praxis ?
Auf jeden Fall mehr
als uns die flüchtigen Spuren des Higgs-Bosons einen Weg aus dem Labyrinth des Teilchenzoos weisen …
Auf jeden Fall mehr
als uns die flüchtigen Spuren des Higgs-Bosons einen Weg aus dem Labyrinth des Teilchenzoos weisen …
Dass
die Kluft zwischen Theorie und Praxis eine tatsächliche ist … 😎
Gast schrieb:
was sagt uns
[quote=Gast]was sagt uns da jetzt für die Praxis ?[/quote]
Daß es kein “zu viel” an Sensorauflösung gibt, entgegen der gängigen Forenmeinung.
Vielen Dank…
Es ist wie im richtigen Leben immer das Zusammenspiel aller am Bild beteiligter Komponenten einschließlich dem Faktor Mensch hinter der Technik die ein gutes Foto ausmachen.
Das Problem ist das jedes Teil für sich optimiert sein sollte. Als Anwender habe ich auf die verbaute Technik aber keinen Einfluss, genau so wenig wie auf die verwendete Software für die Datenverarbeitung innerhalb der Kamera.
Der alte Spruch das alle Theorie grau ist bewahrheitet sich durch diesen Artikel ein weiteres mal. Für mich zählt was als Bild auf der Speicherkarte/PC ankommt.
Theoretisch dürfte bei der Kompakten meiner Gattin gar kein vernünftiges Bild entstehen. Praktischer Weise ist das Gegenteil der Fall. Anscheinend war der Hersteller bei seiner Kompromiss Suche erfolgreich.
Der Aufwand den ich selbst beruflich für eine gute Sachaufnahme betreibe steht in keinem Verhältnis zur einfachen Handhabung vieler DSLR die einem Rückteil immer näher kommen.
Der Artikel war für mich als nicht Physiker oder Techniker gut verständlich und ich wünsche mir mehr Beschreibungen dieser Art bei Photoscala. Schön das es so etwas gibt.
Wieso? Ganz im Gegenteil.
[quote=Gast]
Theoretisch dürfte bei der Kompakten meiner Gattin gar kein vernünftiges Bild entstehen. Praktischer Weise ist das Gegenteil der Fall. Anscheinend war der Hersteller bei seiner Kompromiss Suche erfolgreich.[/quote]
Der Artikel zeigt ja grade, dass nach aller Theorie und Praxis mit einer Kompakten sehr wohl vernünftige Bilder entstehen. Allein das Deppenorchester in den Foren sieht das anders.
Das ist
theoretisch wie praktisch falsch.
Endlich einmal Klartext!
[quote]Weiterhin ist es beim Film so, dass mit jeder zerstörten Verbindung eine Verbindung weniger bleibt, die lichtempfindlich ist. Das heißt, je stärker der Film bereits lokal belichtet ist, desto unempfindlicher wird er an dieser Stelle und die Schwärzung geht in Sättigung. Überbelichtete Spitzlichter werden also nicht radikal abgeschnitten, sondern laufen sanft aus.[/quote]
Endlich einmal Klartext bezüglich der Vorteile von Film, und dazu verständlich formuliert.
[quote]Entscheidend ist: Auflösung schafft Reserven und ist deshalb schlicht durch nichts zu ersetzten. Punkt.[/quote]
Beides sehr gute Gründe, weiterhin Grossformat und Film einzusetzen.
Von Megapixeln: Viel hilft viel
Eine Anordnung von 7 Mikron großen Pixeln liefert eine Auflösung von rund 50 Linien pro Millimeter inklusive der Dämpfung aus Interpolationen und Moiré Effekten. Übliche KB-Objektive bieten solche Auflösungen von bis zu 90 l/mm und der RVP100F zeigt zwischen 80 bis 160 l/mm – abhängig vom Motivkontrast!
Die neugerechneten CCD/CMOS Objektive müssen allerdings noch zusätzlich die Reflexe der Mikrolinsen auf dem Sensor kompensieren und sollten eine “telezentrische” Strahlenführung auch im Weitwinkelbereich unterstützen …
Vielen Dank
Beim Lesen und Begreifen, raucht mir der Kopf,
da ich mit so viel Fachwissen aus diesem Bereich nicht zu Recht komme.
Was ich allerdings in etwa verstehe, sind die Gegebenheiten eines Analog-Digital Wandlers.
Die Umsetzung eines analogen Signales (die Optik ist analog) in ein digitales (der Pixel Chip ist in der Auflösung digital).
Die Angaben der Auflösung eines Chips sind digital, ist ein analoger Wert kleiner
wie für die entsprechende digitale Einheit definiert (z.B. unter 10%),
dann ist dies eine willkürliche Grenze, die zur Zeit der analogen Fotografie Sinn machte,
da es nicht einfach war die Details unter 10% (Kontrast) anzuheben und sichtbar zu machen,
in der digitalen Bildbearbeitung aber, gelingt dies!
Die Auflösung wird anhand von mehreren schwarzen Strichen auf einem weissen Grund beurteilt,
verschwimmen diese zu stark zu einem gleichmässigen Grau,
dann ist ab einem bestimmten Wert die Grenzauflösung erreicht.
Dennoch sehen wir die Striche, (Gegenprobe) denn lässt man in der Gruppe einen weg,
dann sieht man dies!
Weiters ist noch zu bedenken, dass wir selten Gruppen von Strichen fotografieren.
In Realität ist entscheidend, wie lange EIN Strich oder eine Kante sichtbar
und mit Bildbearbeitung noch gut herausgekitzelt werden kann.
Bei Kameras mit extrem hoher Auflösung ist dies durch die Bildbearbeitung eher möglich.
Die Auflösung oder Sampling Rate ist höher.
Oft entsteht aber auch bei falscher Anwendung ein sehr unruhiges Bild.
Eine vierfach höhere Pixelzahl erzielt aber nicht eine doppelt so hohe Auflösung.
Letztendlich ist immer noch wichtig, wie gross ist das Bild und der Betrachtungsabstand.
P.S. Ich finde es schön, wenn man auf ein Foto näher zu geht und dabei noch weitere Details sichtbar werden.
Gut Licht
Kurt
Also:
[quote]P.S. Ich finde es schön, wenn man auf ein Foto näher zu geht und dabei noch weitere Details sichtbar werden.[/quote]
Also Grossformat und einen Fuji Provia 100F oder Velvia 50 für Farbe. Oder für s/w 6×9 und den Adox CMS 20: http://www.adox.de/ADOX_Filme/Premium%20Line%20Films/ADOX_CMS_Filme/ADOX_CMS_Filme/ADOX_CMS_Filme_Bildbbsp.html
Der Artikel erreicht nicht die erforderliche…
…Bandbreite für Erkenntnisse die auch noch dann Bestand haben, wenn man die richtigen Fragen stellt.
Unabhängig davon ist der CCD-Typ eine analoge elekronische, flächige Abtasteinheit. Sog. Eimerkettenschaltungen und Ladungsschienen liefern die Ladungen zu hochwertigen Wandlern. Diese Signalverstärker wandeln das Ladungsgebirge in einen analogen Spannungsverlauf. Danach wird A/D-gewandelt.
CMOS funktioniert wie ein Speicherbaustein nur eben werden anstatt 0 und 1 eben die Pixelwerte in Form von analogen Spannungswerten aus dem Pixelarray ausgelesen und erst außerhalb des Pixel-Array A/D-gewandelt.
Bei großen CMOS-Sensoren stört weniger das thermische Rauschen sondern das sporadische Rauschpattern durch Millionen kleiner mit Toleranzen behafteter Spannungsverstärker direkt am Pixel. Blauer Himmel wäre ohne Rausch-Pattern-Hobel-Tricks per Software schlichtweg total verrauscht und das am hellichten Tag bei besten Lichtverhältnissen.
Nokia erledigt beim 808 PureView tatsächlich gem. dem Motto “Viel hilft viel” dieses sporadisch Rauschpattern was man va. in Himmelflächen sieht. Hier ist ein FFT CCD von Natur aus sauber und muss nicht per Rauschpattern-Hobel-Software gereinigt werden. Das CDS-Verfahren von CMOS-Sensoren wirkt hier NICHT, denn der Fehler kommt erst nach dem CDS-Verfahrens-Schritt dazu.
Jeder Struktur-Typ seitens des Motivs wird untersch. gut oder schlecht von den nach der elektronischen, flächigen, analogen Abtastung behandelt. Das incl. Bayer-Pattern-Transfer, etc.. Schwarz-Weiss-Linien und der Umgang durch das System damit sagt nicht alles aus auch nicht, wenn man neben banalen MTF-Kurven sogar noch die Modulationswerte-Kurve über den gesamten Ortsfrequenzbereich vom Sensor vorliegen hat.
Unterm Strich. Hier ist noch viel Gold vergraben und das letzte Wort ist noch nicht gesprochen.
Was jedoch ganz klar steht ist, dass der CCD-Typ v.a. der FFT CCD-Sensor der Sensor ist an dem am wenigsten herumexperimentiert wird sondern ganz klar eine Linie entlang seiner klaren Stärken verfolgt wird. Seitens der optischen Eigenschaften die Referenz und wenn man weiß wo man hingucken muss bleibt auch die Nikon D800 ein netter Versuch digitales Mittelformat oder eine Leica M9 mit FFT CCD ersetzen zu wollen. FFT CCDs durchzeichnen Details schlichtweg homogener und sauberer. Bildeindruck aus dem typ. Betrachtungsabstand ist räumlicher, plastischer und bei Annäherung wird das nochmals deutlicher. CMOS bzw. Active Pixel Sensoren incl. LiveMOS wirken “verwaschen” und in feinen Strukturen fusselig und teilweise pixelig.
Was den Vergleich mit Film betrifft, zieht ein Farbnegativ-Film eben Schatten zu und belichtet man nach kommt das Filmkorn zum Vorschein anstatt durchzeichnete Details. Dafür ist die Tonwertkurve in Lichtern sehr weich, während ein Sensor ohne weitere Massnahmen eigentlich eine harte Tonwertkurve besitzen würde. Beim FFT CCD beläßt man das i.d.R. auch, denn große FFT CCDs haben genügend Dynamikumfang. Beim CMOS bis auf z.B. den CMOS der Nikon D3 erhält man einen erweiterten eigentlich nicht existenten Dynamikumfang durch Überschussladungs-Abflüss-Drainagen direkt am Ladungstopf der Pixel. Dadurch ergibt sich messtechnisch eine weiche Kennlinie. In Ladung gewandelte Photonen, dh. eine bestimmte Licht- und damit auch Informations-Menge wird vom Sensor und damit dem System weggeworfen um eine künstliche in Lichtern gekrümmte Tonwertkurve zu erhalten und spontan bunte Lichtkringel um Spitzlichter zu vermeiden.
CMOS-Sensoren in APS-C bis KB-VF-Kameras sind im Vergleich zu jeder Kamara mit Profi FFT CCD schlichtweg ein Witz. Hierfür gibt es bisher scheinbar keinen Anreiz für genauere Untersuchungen, denn bei jedem Kameratest sind eben die HighISO-Samples in den Samples-Gallerien der Anreiz der Untersuchungen schlechthin.
Ich fotografiere immer noch mit meinen sog. Highend-Kameras mit 5…10MPx und CCD bzw. FFT CCD und sehe bei der Bearbeitung ein Bildmaterial, welches mir einfach besser schmeckt als das aus den CMOS-Knipsen. Beugungserscheinungen sind mir da auch bei f16..22 und kleineren Blendenöffnungen sowas von Wurst. Der Bildeindruck wirkt nicht verwaschen wie bei CMOS von der größen Blendenöffnung weg, sondern man sieht eben die Physik so als würde man mit Film fotografieren. f8 bei 1/1,8-Zoll-Sensor ist eben wie f22…f32 bei KB-VF. Und nichtmal das. Viele Objektive auf digitalem KB-VF sehen im Bereich f22…f32 deutlich unschöner aus als f8…f11 bei 1/1,8-Zoll-Systemen. Und mit “Viel hilft viel” kriegt man die Artefakte auch nicht weg. Nicht falsch verstehen. Ich fotografiere nicht nur mit 1/1,8-Zoll-Systemen. Und bei der Rangefinder-Kamera bin ich noch Analog mit Film und Leica M-Bajonett unterwegs.
wird also
mit jedem Schließen der Blende – die erreichbare Auflösung weiter begrenzt…
?
Korrekt.
Hängt aber von Objektiv ab. In der Regel begrenzen bei großen Blendenöffnungen die Linsenfehler die Auflösung. Je weiter man abblendet, desto geringer werden die Linsenfehler, wobei gleichzeitig die Beugung die Auflösung immer weiter begrenzt. Oft hat man dann ein Optimum in der Gegend von f/5,6 – f/10,0, bevor die Beugungsbegrenzung überwiegt.
Bei der XZ-1 z.B. wird die Beugungsbegrenzung bei f/4,0 bereits sehr deutlich sichtbar. Offenblende (f/1,8-f/2,5) oder f/2,8 gibt die schärfsten Ergebnisse; d.h das Objektiv ist sehr nah an der Beugungsgrenze gebaut oder sogar beugungsbegrenzt.
Ja, natürlich
Ist ja auch im oben abgebildeten Diagramm gut zu sehen – wenn
man will … 😎
Um es noch mal zu sagen:
die Auflösug wird niemals begrenzt, die bleibt immer gleich.
Was sich verändert, ist die Fähigkeit, restlos scharf abzubilden, und zwar von der Bildmitte ausgehend immer weniger scharf bis zum Rand.
Scharf ist aber relativ, vor allem wenn man es mit digitalen Bildern zu tun hat. Wir bekommen ja nicht ein “pysikalisches” Bild, sondern ein gerechnetet. Allein, was die Software in das Bild hinein dichtet, lässt alles, was hier an “Beugungsunschärfe” diskutiert wird, albern aussehen. Bilder werden i. d. R. “scharf” gerechnet, also Effekte wie Kantenschärfung (unscharf Maskieren) bis Kontrastanhebung und was es sonst noch so alles im Arsenal der Programmierer gibt, produzieren letztendlich dsa Bild.
Für die krasse überwiegende Mehrheit der Bilder ist es eher besser, etwas Schärfe heraus zu nehmen. Man darf nie vergessen, dass die Sensoren erst mal einfach nur hell/dunkel sehen. Zu jedem Pixelort müssen min. 2 Farbangaben dazu definiert werden, für die es keine wirklich messbaren Aussagen gibt. Das funktioniert rechnerisch sehr gut.
Das gleiche gilt dann auch im Umkehrschluss beim Drucken. Der Drucker/Belichter gibt nicht immer alles aus, was in den Daten eigentlich drin steht. Allein wenn man sich beispeilsweise die Kacheln der JPGs anschaut (Druck-PDFs sind in der Regel immer JPG-Ausgabe), glaubt man gar nicht, dass das dann jemals ein tatsächlich als richtig empfundenes Bild ergibt. Und das auch noch in aller Schärfe. Wenn man dann ein in der Regel sehr viel kleineres digitales Bild (an ausreichender Auflösung mangelt es in dem Fall fast immer) auf eine finale Größe projeziert, wird endgültig klar, dass in den Algorithmen, die der Druckertreiber verarbeitet, einiges passiert.
Oder anders, wenn im Offset bei einem 300 dpi auflösenden Bild im symetrischen Raster eine ganze Menge an Bildpunkten, die vorher da waren, schlicht und einfach durch das Raster geschluckt wird, aber das Bildergebnis hinterher trotzdem als hochwertig scharf empfunden.
Einfach nur nicht kirre machen lassen. Ausprobieren, was geht und dann das nehmen, was einem wirklich gut zur Hand geht und sich nicht durch pseudotheoretische Kaffeesatzleserei verrückt machen laasen.
Für die Praxis leider absolut verfehlend!
Altbekanntes mal wieder aus dem Physiklehrbuch abgeschrieben und aufgepeppt!
Perfekte Optiken, nur begrenzt durch die Beugung, existieren tatsächlich.
Mann oh Mann! Absolut verfehlend für alles, was an Objektiven für den kaufkräftigen Konsumenten angeboten wird bzw. der Markt tatsächlich an Erschwinglichem selbst für den Profi hergibt! Da hilft selbst der Hinweis auf einen wahrhaftigen Doktortitel des Verfassers leider nix!
Zum einen
steht da nix von “für den kaufkräftigen Konsumenten”, zum anderen überleg Dir mal selber wie nahe z.B. ein Handyobjektiv an der Beugungsgrenze konstruiert sein muss, damit man bei einer Pixelgröße von ~1 µm, also ~500 Pixelpaaren pro Millimeter, noch was von seiner hohen Auflösung hat, also um noch einen sinnvollen Kontrast bei 500 lp/mm – ähm, pp/mm – zu erzielen. Ich geb’ Dir’n Tipp: Nicht umsonst haben diese Objektive eine Lichtstärke von 2,8.
Also verstehe die Reaktionen
Also verstehe die Reaktionen wie diese mal wieder gar nicht, da macht sich einer mal die Mühe und liefert den theoretischen Hintergrund mal sachlich und so verständlich als möglich aufgearbeitet und, zum Glück nicht alle aber meiner Ansicht nach doch zu viele Beiträge hier regen sich drüber auf das hier Schwadroniert würde. Wen das stört, oder wer das so sieht – nicht lesen hilft!
Warum dennoch hier über den Autor abgelästert wird, da kann ich nur mutmaßen, was ich aber lieber unterlasse denn wirklich positive Gründe kommen mir gar keine in den Sinn. Denn sollte hier grundlegend etwas falsch dargestellt worden sein, dann formuliert doch bitte den Einwand einfach sachlich, dann wäre der Beitrag auch für etwas gut. Und wenn das so langweilig und altbekannt ist, dann doch erst recht, warum lesen?
Abgesehen davon, es ist es schon klar das dieser Beitrag hier auf einen anderen Artikel hin geschrieben wurde, das da ein Bezug besteht?
———-
Danke für die Mühe an den Autor der sich hier Mühe beim Versuch gegeben hat hier bei diesem Thema ein paar grundlegende Dinge zurechtzurücken.
Wo viel Licht ist, ist starker Schatten…
…und wahrscheinlich wird man für jeden Umstand einen gesonderten Sensor brauchen.
Vielen herzlichen Dank für Ihre Mühe, den sehr lehrreichen Artikel, und Ihre Bereitschaft Ihr Wissen zu teilen.
Grau ist alle Theorie,
meint der Profifotograf.
Ewas hilflos.
[quote=Randolf Butzbach]Die anderen argumentieren etwas hilflos, dass es vor vielen Jahren mal einen Film namens Agfa-Ortho 25 gab, mit einer extrem hohen Auflösung, und da hätte schließlich auch keiner nach der Qualität der Objektive gefragt.[/quote]
Ich lege Wert auf die Feststellung, dass mein Verweis auf den Agfa Ortho 25 vor einigen Wochen nicht “hilflos” war.
Vielmehr handelte es sich um den Versuch, in einem Forum, welches nicht ausschließlich von Universitätsprofessoren und anderen Vertretern der intellektuellen Oberschicht getragen wird, in einfacher Sprache zu verdeutlichen, dass einige der gegenüber Kameras wie der D800 vorgebrachten “Killerargumente” barer Unsinn sind. Hier werden schon seit der Erstankündigung dieser Kamera und ihrer Sensorauflösung von selbsternannten Experten Argumentationslinen gezimmert, welche beim technisch unbedarften Leser den Eindruck erzielen können oder sogar wollen, dass diese Kamera mit dem Großteil der verfügbaren Objektive schlechtere Ergebnisse erzielen würde als eine Kamera geringerer Auflösung bzw. dass für den Einsatz dieser Kamera erst geeignete – und nach der Einschätzung der Autoren kaum oder nicht verfügbare – Objektive anzuschaffen seien. Eine Argumentation, welche für extrem hoch auflösende Filme, für die der genannte nur willkürlich und beispielhaft angeführt wurde, nicht historisch dokumentiert ist. Zumindest wäre mir als Gerade-Noch-Zeitgenosse des Agfa Ortho 25 und einiger vergleichbarer Filme eine solche Diskussion nicht erinnerlich.
Zitat
“Die Hohe Kunst des Sensorbaus besteht also jetzt darin, die sich widerstrebenden Eigenschaften Ortsauflösung (Megapixel) einerseits und Intensitätsauflösung (Dynamikumfang) andererseits durch konstruktive Tricks zu „versöhnen“ und für die jeweilige Anwendung den besten Kompromiss aus beiden zu finden.”
Worüber “diskutieren” hier alle noch um den heißen Brei herum? Oder liest hier jeder heraus, was ins gerade genehme Weltbild passt!?
Physiker können
Physiker können Fotogruppen, die aus Nerds und Geeks bestehen und im wesentlichen Kamerakäufe und -verkäufe diskutieren , wertvolle technische Impulse geben:
Ich erinnere mich noch an Vorträge über laminare Strömungen in Jobo-Tanks, Photomultiplier in der Laborbelichtungsmessung, Verzeichnungsfreiheit des 50er Summicron, Theorie der Zweibadentwicklung in Emofin, Dokumentenfilme in Neofin Doku usw.
Das war alles interessanter, als sich endlose Diavorträge mit schlechten Fotos anzuschauen.
Der Rolleiflexer
Um es nochmal zu sagen….
eigentlich ist es mir wurscht wo und mit was ein Bild gemacht wurde wenn es die gestellten Anforderungen erfüllt. In den Jahrzehnten meiner beruflichen Fotografie hat noch nie ein einzelnes Teil meiner Ausrüstung DAS Foto ausgemacht es war immer die Summer aller Beteiligten bis hin zum Druckerzeugnis.
Selbstverständlich habe ich darauf geachtet jeweils die besten momentan verfügbaren Werkzeuge miteinander zu verknüpfen. Als Anwender habe ich keinen Einfluss auf verbaute Technik und die verwendete Software zur Verarbeitung der digitalen Daten bis sie auf dem Rechner landen.
Ab diesem Zeitpunkt haben die Beteiligten an der Produktion Zugang auf den weiteren Prozess. Alles was vorher hinter verschlossener Tür / Kamera abgelaufen ist war graue Theorie und ist vom Anwender nicht beeinflussbar.
Trotzdem ist es schön wenn ich einen Teil dieses Prozesses verständlich erklärt bekomme. Manchmal hilft solches Wissen Fehler zu vermeiden. Wenn es jetzt noch so einen verständlichen Artikel über die Datenverarbeitung innerhalb der Kamera zum RAW Bild gäbe, dann könnte das für die praktische Arbeit von Vorteil sein.
Nochmals vielen Dank.
…
“In beiden Fällen ist dann aber irgendwann plötzlich Schluss: Der Kondensator ist vollständig ge- bzw. entladen, was dazu führt, dass (überbelichtete) Spitzlichter schlicht abgeschnitten werden. Da Elektronen unteilbar sind, also eine diskrete Anzahl Elektronen gespeichert ist, werden beim Auslesen des Sensors die gespeicherten Elektronen ausgezählt. D.h. das im Sensor gespeicherte Signal ist bereits von Natur aus digital. Folglich ist es (abgesehen von Marketinggründen) sinnlos, die Bittiefe des sogenannten Analog-Digital-Wandlers (ADC) zu vergrößern, wie immer wieder in den Foren gefordert wird. Der ADC kann keine größere Anzahl verschiedener Werte abliefern, als im Sensor Elektronen „produziert“ und gespeichert werden können.”
Schön gemogelt…
MfG
__________________________________________
Wissen ist Macht.
[Francis Bacon, 1561 – 1626]
ETTR
Expose To The Right der CCD oder CMOS Photodioden stellt für mich eine besondere Herausforderung dar. Während ich für die Silberhalogenid basierten Filme die richtige Belichtung anhand der Lichtwerte prima mit den Augen einzuschätzen vermag, bin ich bei den Foto-Halbleitern stets auf mühsame Belichtungsreihen angewiesen. Nur so kann ich ein “clipping” oder “banding” durch schlichtes Ausloten – insbesondere bei hohen Motivkontrasten – dämpfen!
Michael Reichmann hat diese Belichtungsproblematik in der Digitalfotografie sehr treffend – wie ich finde – skizziert:
http://www.luminous-landscape.com/tutorials/optimizing_exposure.shtml
Vielleicht mögen Sie mit dem Thema “Optimales Belichten von MegaPixeln” an ihren obigen informativen Artikel anknüpfen?
Belichtungstechnisch
ist das tatsächlich eine Herausforderung. Das war’s aber bei Dias auch schon – allerdings ohne RAW-Reserven.
Gerade deswegen: Solides Handwerk statt digitalem Automatik-Kult!
Ganz so problematisch
ist es auch nicht. Problematischer sehe ich die Fixierung der Hersteller, die kamerainterne Belichtungsmessung und -anzeige immer noch auf Basis der Analog-Fotografie vorzunehmen. Das gedanklich zu kompensieren macht die Arbeit unnötig komplitziert(er).
Bei allem Respekt,
aber der Michael Reichmann ist ein Fotograf, der sich von einem Programmierer (oder meintewegen auch Physiker) die Bit-Welt hat erklären lassen und jetzt schaltet er seinen gesunden EV-Welt-Verstand aus und geht damit die Welt bekehren.
Sicher, “Expose to the right” ist richtig und wichtig, wenn ich Wissenschaft machen will. Da will ich maximalen Dynamikumfang, und zwar ohne dass irgendwas abgeschnitten wird, weil ich es dann ggf. nicht mehr auswerten kann. Da mache ich dann auch “Probebelichtungen” und schaue, dass nirgends irgendwas abgeschnitten wird.
Den Aufwand kann und will ich mir beim Fotografieren aber nicht leisten: Da will ich drauf vertrauen, dass auch (überbelichtete) Spitzlicher noch möglichst im Dynamikumfang des Sensors bleiben. Von daher gehen die Belichtungsreserven, die sich durch “Belichten wie Film” ergeben, schon in Ordnung. Wenn Sie dagegen den vollen Dynamikumfang des Sensors ausreizen wollen, dann bleibt Ihnen in der Tat nichts anderes übrig, als soviele Probebelichtungen zu machen, bis grade keine Lichter mehr abgeschnitten werden.
Abgesehen von der Tatsache, dass Ihnen bis dahin vermutlich ihr Motiv weggelaufen ist, kann Sie das vor das Problem stellen, dass Sie es dann geschafft haben, dass die Lichter zwar vollständig im Dynamikumfang liegen, dafür das Haptmotiv im Rauschen absäuft wenn der Unterschied zwischen hellsten Reflexen/Lampen und Hauptmotiv zu groß wird.
Von daher wird das, was wir in den Jahren der manuellen Belichtung gelernt haben, und was die Kamera versucht zu imitieren, nicht ungültig, nur weil da jetzt ein Sensor dran hängt.
Im speziellen Einzelfall können Sie dann ja immer noch eine Belichtungsreihe machen und die Reserven zugunsten des Dynamikumfangs freigeben.
Ansonsten, wenn Sie die Reserven absolut nicht haben wollen, lassen Sie die Belichtungskorrektur einfach auf +1 EV oder, wenn Ihnen alles egal ist, gar +2 EV stehen und dann haben Sie den Mittelwert an den rechten Rand geklatscht.
Zur Erinnerung: Im 8-Bit-JPEG-Histogramm liegt der Mittelwert bei 127, der maximal darstellbare Wert ist 255. Ein EV, also eine Blendestufe oder ein Bit mehr, macht aus 127 den Maximalwert von 255. Mit +2 EV, verschieben Sie das Histogramm um zwei Bit, machen also aus der 63 eine 255.
Schwierig
Es ist schon schwierig, in einem solchen Forum einen intelligenten Artikel zu platzieren!
Die dumme Masse hält mit Vehemenz dagegen. Und noch schlimmer: Alle totgeglaubten Schreiberleichen trumphen plötzlich als Grufties wieder auf….
Schwierig scheint es
den Unterschied zwischen Theorie und Praxis ausreichend rüber zu bringen …
Die Technik ist ok
Das Problem ist heute nicht mehr die mangelnde Qualität der (digitalen) Technik,
sondern (zum Glück) wieder, wie einst zur analogen Zeit, die Fähigkeiten
des Fotografen.
Heute dreht jeder Amateur die Regler an der Kamera und bei der Software
in Richtung Plus, daran erkennt man ihn.
Der wirkliche Profi holt aus einer digitalen Kamera, wie einst zur analogen Zeit,
die Qualität heraus die möglich ist und das ist auch digital möglich!
Qualität lässt sich nach wie vor, nicht mit hohem Kontrast, saftigen Farben usw. MACHEN!
Gut Licht.
Der Profi zeigt sich auch in der digitalen Fotografie
Kurt
GUT LICHT :-)…
& gut druck … habe mit allerfeinsten paradeiser`brot und an glaserl veltliner -die- postings gelesen ~ huijh … kaiser`schmarrn ist nix dagegen ! …
keiner / e der beiTragenden hat selber`mal ein`sein… oder sonstiges -photo- auf zb. A1 ausgedruckt ( zz. HP 130 design jet 12oo x 16oo dpi ) oder 😉
ein -photo- A1 / 600 x 600 dpi hat in corel compression 1003 MB ! dass auf echte leinwand gedruckt ( in einstellung – photodruck ? dauert ca. 18 stunden ??? )
nur dass man(?) / Frau über nix`wissen ! sooo`viel -nix- schreiben kann ist dass faszinierende daran ( satire pur ! ) ~ danke
mit vorzüglicher hochachtung – nur ijh dah ralf …
ps… mit sony DSC H3 / 8 MB / format A1 … lol
http://kunst.creative.arte.tv/de/gallery/users/731/ralf-purkart
Das wird hier auch nicht bezweifelt,
allerdings gewinnen gute Fotos immer durch eine sachkundige technische Umsetzung sowohl bei der Aufnahme als auch hinsichtlich der Weiterverarbeitung in der Dunkelkammer oder am Rechner! Als Fotoamateur brauche ich nicht kundenorientiert oder effizient zu verfahren. Am Ende möchte ich nur ein SW-Bild in den Händen halten, welches ausschließlich meinen Ansprüchen als Amateur genügt. Beispielsweise lässt sich der von Oberflächen-Entwicklern bekannte Eberhard-Effekt sehr viel kontrollierter am Rechner nachträglich ergänzen, wenn man die Filter (hier: Hochpass) motivgerecht einzusetzen vermag. Und die Erkenntnis, was denn “unter der Haube” als Algorithmus abläuft, kann manchesmal auch sehr hilfreich sein.
Warum sollte man sich im Netz nicht über MegaPixel, ETTR, digitale Filter oder neue Entwickler für “Tabular Grain” Suspensionen austauschen?
Der Amateur sorgt sich um seine Fotoausrüstung, der Profi um neue Kundenaufträge und der Meisterfotograf um das Licht …
Gast schrieb:
Heute dreht
[quote=Gast]Heute dreht jeder Amateur die Regler an der Kamera und bei der Software
in Richtung Plus, daran erkennt man ihn.[/quote]
Früher nannte man das Velvia.
Danke für den Artikel
Danke für den Artikel. Ich werde den zwar noch 2 – 3 mal lesen müssen, bis ich alles verstanden habe, das ist es mir aber Wert.
@alle: es gibt halt die Künstler, die Fotos machen und die Ingenieuere, die hierfür die Werkzeuge machen. Diese “Werkzeugmacher” müssen die genutzte Physik verstehen ansonsten ist es nur rumstochern im Nebel. Fussball-Parallele: der Trainer schiesst keine Toore. Aber ohne Trainer machen die Spieler keine Toore.
signifikante Auslösungsverbesserung durch mehr Pixel ?
“Je höher die Pixelauflösung des Sensors ist, desto genauer kann also das Bild aufgezeichnet werden und desto feinere Informationen können herausgearbeitet werden.”
Wenn ich das richtig verstanden habe, ist in Abb.9 die Pixeldichte 16fach, was tatsächlich zu eine höheren Auflösung als Abb. 8 führt.
Wiviel Pixel müßte ich denn auf einem APS-C Sensor haben um eine sichtbar bessere Auflösung als bei 16 MP zu haben, 256 MP ?
Und wenn ich richtig verstehe müßßten dann 16 Subpixel zu einem Bildpixel zusammengerechnet werden um dann ein hochaufgöstes 16MP Bild zu erhalten?
Gruß Udo